August 1998
<<July August September>>
2005: Fuxiang Yu sent in a much improved solution to this puzzle:
Read Fuxiang Yu's solution (89KB)
2012: Zhong Nan and Sandy Jelly sent another simpler solutions:
Read Zhong Nan's solution (114KB)
Read Sandy Jelly's solution (150KB)
2016: Alek Vainshtein sent another nice solution:
Read Alek Vainshtein's solution (24KB)
2020: Yang Haibo, a physics teacher from China, sent us yet another solution:
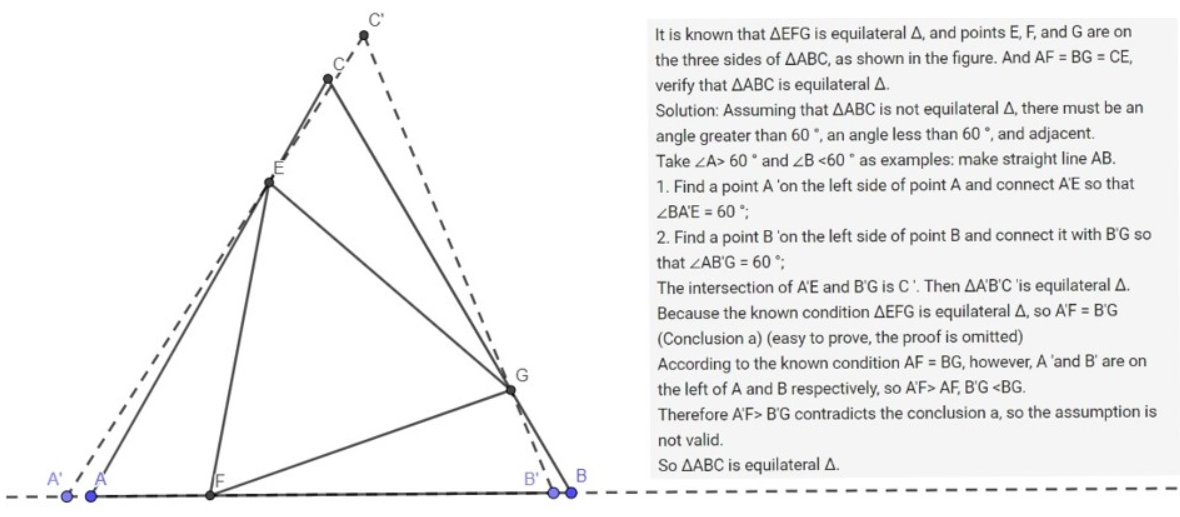
Most of the submited solutions demonstrated the fundamental challenge of this problem: How do you prove something that seems obviously true? The problem’s simplicity and the intuitive “obviousness” of the conclusion lead many responders down dead end paths. Some suggested using trigonometric functions to prove triangle ABC equilateral, but none of the other triangles present are implicitly “right” triangles. Others began with the assumption that triangles ADF, BED, and CFE were congruent, which cannot be assumed, but rather needs to be proved.
Here is our solution. Click ![]() for the IBM techexplorer version.
for the IBM techexplorer version.
Our earlier posted solution follows. We proceed by breaking into cases. Let the sides of DEF have length x, and the line segments AD, BE, and CF have length y. The form of our solution will depend on the value of y/x. We begin with some special cases. The following Diagram is referenced for Case 1 & 2.
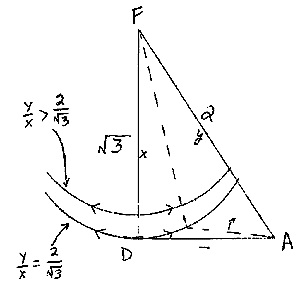
Case 1, when y/x = 2/SQR3
In this case the largest value possible for angle A would be 60° --when angle ADF = 90° (see diagram). Since AD = BE = CF, this holds true for triangles BED and CFE as well. In this case then, since angles A, B, and C must sum to 180° , they must all be 60°, and ABC equilateral.
Case 2, when y/x > 2/ SQR3
In this case, as x grows smaller (or y larger, or both) Angle A only grows smaller (see diagram). Again, since this is occuring equally throughout triangle ABC (AD = BE = CF, and triangle DEF is equilateral), angles A, B, and C must be under 60°, which makes it very difficult for them to sum to 180°. So case 2 is not possible.
Case 3, when y/x = 1, or when triangle ADF is isosceles.
For convenience, lable the angles as follows: ADF = beta, FAD = A, DFA = gamma, CFE = delta, and BED = epsilon. We know that gamma = A = 90° - beta / 2. This implies that delta = 180° - (gamma + 60°). Substituting (90° - (beta / 2)) for gamma, we get delta = (beta / 2) + 30°. Similarly, epsilon = (delta / 2) + 30°, and beta = (epsilon / 2) + 30°. The system of linear equations has the unique solution beta = >A = gamma = delta = epsilon = 60°. in particular A = 60° , and the same argument implies that all three angles of the large triangle are 60° and it is therefore equilateral.
Case 4, when 0 < (y/x) < 1
Consider fixed values of x, y with 0 < y < x. Concentrate first on the triangel DAF, where we label the angles as in case 3 above and two sides are fixed at FD = x, DA = y. Let beta range from 0° to 180° and notice what happens to A and gamma. As beta increases, AF increases (by the law of cosines), and A decreases from 180° to 0°. By the law of sines, gamma at first increases from 0°, but when A hits 90°, gamma starts decreasing (if plotted on a graph, gamma’s range would describe a parabola).
So there is exactly one value of beta, call it beta 0, which makes A = 60°. Let the angles in this case be called A0 = 60° and gamma0 = 180° - beta 0 - A0. We would have delta0 = 180° - 60° - gamma0 = beta0. Then each angle of the large triangle is 60° and it is equilateral.
Suppose that all three angles beta, delta, epsilon, are smaller than beta0. Then each of the three angles A, B, and C is larger than 60°, and so can’t sum to 180°.
The only other possibility is when the largest of the three, say beta, is larger than beta0. Then A < A0 = 60° < 90° so that gamma < gamma0 , and delta = 180° - 60° - gamma is also larger than beta0 . By the same argument, epsilon > beta0 . Then each of the three angles A, B and C is smaller than 60° , and again they can’t sum to 180°.
So, in this case, the only consistent conclusion is when beta = beta0 and the large triangle is equilateral.
Case 5, when 1 < (y/x) < 2 / SQR3
This last case is somewhat easier than # 4 above. Consider a movable triangle as before, but remember that y > x . So as beta grows from 0° to 180°, we notice that gamma shrinks from 180° to 0°, and delta grows. This means that beta, delta, epsilon must all be the same; if delta were larger than beta, than (by monotonicity) epsilon would be larger than delta, and beta would be larger still, which would yield a contradiction. If beta, delta, and epsilon are the same, then by side-angle-side, the three triangles ADF, CFE, and BED are congruent, so the outer angles A, B, and C are equal, and the large triangle is equilateral.
If you have any problems you think we might enjoy, please send them in. All replies should be sent to: ponder@il.ibm.com