Ponder This

September 2025 - Challenge

<< August September

Let’s say we have a round strawberry cake with chocolate icing on top and an angle \theta with the range 0<\theta<2\pi. We then perform the following procedure: We successively cut wedges of angle \theta from the cake, and each time we cut a wedge, we flip it and re-insert it upside down into the cake, at first with the icing at the bottom (we can picture it as if the wedge magically re-attaches it to the cake).

For example, if \theta = \frac{\pi}{2}, then the following image displays the various stages the cake goes through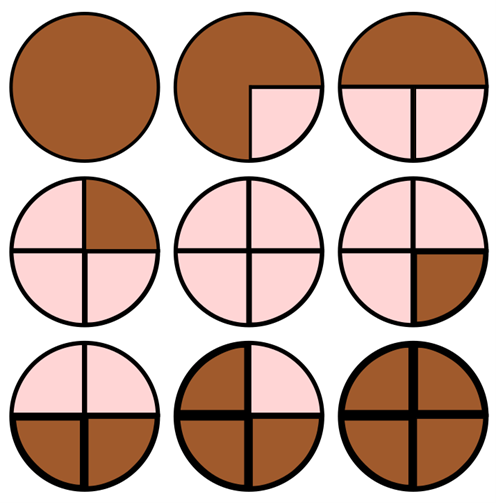

In this example, after four steps, all the icing is now at the bottom of the cake, and after eight steps, all the icing has now returned to the top of the cake.

Your goal: For \theta = e^{-10} where e=2.718\ldots is the usual constant, find the number of steps it will take for all the icing to return simultaneously to the top of the cake for the first time, or provide an explanation why this will never happen.

A bonus "*" will be given for finding the number of steps that will take for all the icing to simultaneously get to the bottom for the first time, or provide an explanation why this will never happen, for the same value of \theta.

We will post the names of those who submit a correct, original solution! If you don't want your name posted then please include such a statement in your submission!

We invite visitors to our website to submit an elegant solution. Send your submission to the ponder@il.ibm.com.

If you have any problems you think we might enjoy, please send them in. All replies should be sent to: ponder@il.ibm.com