September 2025 - Solution
September 2025 Solution:
The solution to the main puzzle is 38307182424. The solution to the bonus is "never".
This puzzle is more tricky than most, in the sense that experienced math puzzle solvers are more likely to fall into its trap: It seems that since the step is of irrational length, we will never return to the starting point, and so there's no hope to re-flip everything. The even more sophisticated solvers note that since we use the angle \frac{1}{2\pi e^{10}} the solution hinges on the unproven claim that \pi e^{10} is irrational. These intuitive (for the seasoned math problem solver) ideas are completely irrelevant to the solution.
The key observation here is that when we flip a wedge, we do not simply change its status from "icing up" to "icing down" and vice versa; we mirror the cuts currently present in the wedge. This can be seen easily if we look at an example where the cuts do not return to the origin after one spin, e.g. when \theta=\frac{3\pi}{2}:
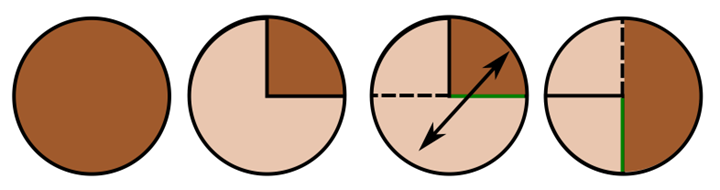
One easy way to perform the bookkeeping of the current location of the cuts is to think of the following equivalent formulation: The knife always cuts a line at the angle 0 (e.g. horizontal line going right from the center). After each cut and flip, the cake is rotated by \theta degrees. So an algorithm for generating the set A of the angles of all the current cuts in the cake is
- Initialize A ← {0}
- For x ∈ A:
- If 0 ≤ x < θ: x ← (θ - x)
- A = A ∪ {(x + θ) % 2π}
- Goto 2 if A changed, else return A.
Let k=\lceil\frac{2\pi}{\theta}\rceil be the smallest number of steps required to perform at least a full circle. Than \delta=k\theta-2\pi is how much we "overshoot" a full circle each time. It is now easy to check that in the above algorithm, the resulting A would be
A = \{0, \theta, 2\theta, \ldots, (k-1)\theta, \delta, 2\theta-\delta, 3\theta-\delta, \ldots, (k-1)\theta-\delta\}
Where the elemnts of A are presented in the order in which they are obtained from the previous one. After rotating (k-1)\theta-\delta by \theta we arrive at (k\theta-\delta) \text{ mod } 2\pi = 0, hence in this sense we "complete a full circle" even though \theta may be irrational.
Since |A|=2k-1 we can picture the cake at the beginning as being comprised from 2k-1 wedges, of which k have an angle of \delta and k-1 have an angle of \theta-\delta:
[0,\delta], [\delta,\theta], [\theta,2\theta-\delta], [2\theta-\delta, 2\theta],\ldots,[(k-1)\theta,0]
Each time we cut and flip the cake, we flip exactly one \delta-wedge and one \theta-\delta-wedge while switching the order between those two wedges but keeping the original order between all \delta-wedges and \theta-\delta-wedges. Hence, after k cuts we completely flip all the \delta-wedges and after 2k cuts we return them all to their original orientation, and similarly with the \theta-\delta-wedges and k-1 cuts.
In general, for the \delta-wedges to be all down we need the number of cuts to be an odd multiple of k, and for up we need an even multiple. Similarily with \theta-\delta-wedges and multiples of k-1. This leads to the solutions:
- 1. The icing returns to the top when the number of cuts is an even multiple of both k and k-1. Since \text{lcm}(k,k-1)=k(k-1), and since when k is even k-1 is odd and vice versa, the smallest number which is an even multiple of both these numbers is 2k(k-1). When \theta=e^{-10} we have k=138397 and 2k(k-1)=38307182424.
- 2. Since one of the numbers k,k-1 is always even, there is no joint odd multiple of both of them, hence the icing will never be completely at the bottom (again, contrary to the intuition that it should happen at the middle point before everything returns to the top).