Ponder This

August 2025 - Challenge

<< July August

Alice and Bob play the following game: Given a grid of a\times b squares, if it is Alice's turn, she uses vertical cuts to split the grid into two or more grids of the same size; if it's Bob's turn, he does the same with horizontal cuts. The cuts can be performed only on the edges of the grid squares, not on the squares themselves.

For example, given a 4\times 6 grid, Alice has three possible moves that can split the grid into two 3\times 2 grids, three 4\times 2 grids, or six 4\times 1 grids. Bob can either create two 2\times 6 grids or four 1\times 6 grids:

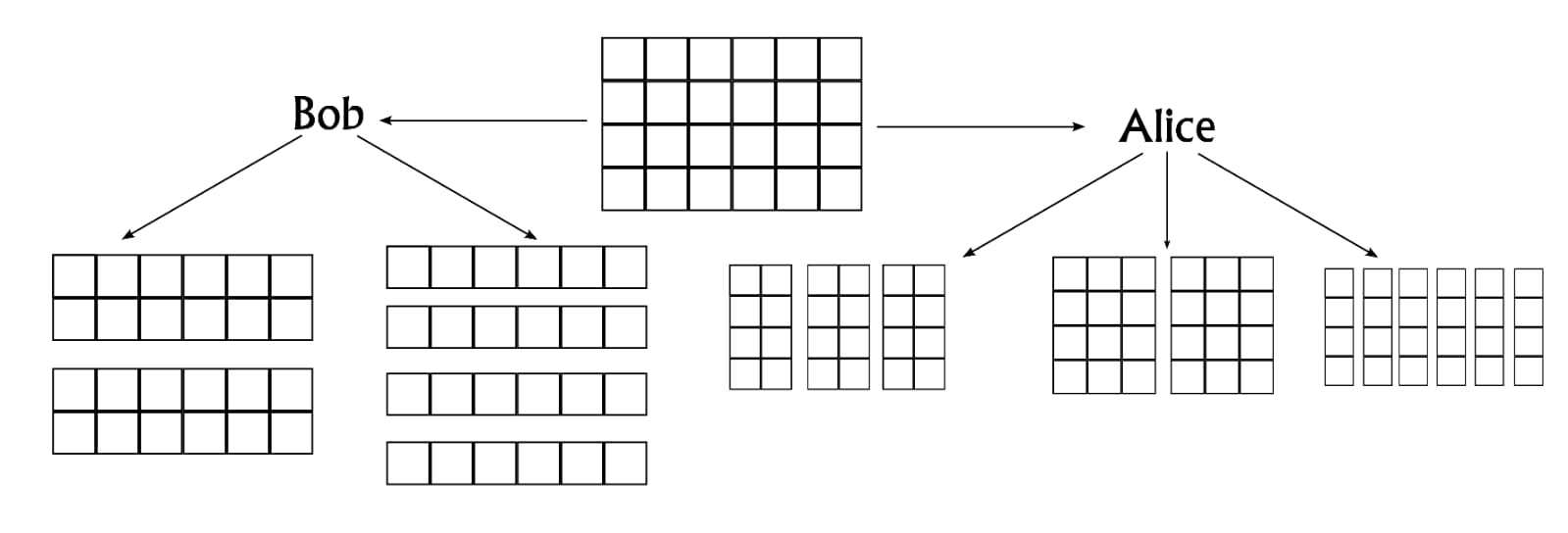
In the general game, Alice and Bob alternate turns. There can be several grids in play at once, and during each turn, the player chooses a grid and cuts it according to the above rules, replacing the grid with their newly created ones. A player loses if it’s their turn and they cannot cut any grid. For example, if the game consists of four 1\times 6 grids and it's Bob's turn, Bob loses since he has no move that will split an existing grid into two or more grids.

We assume that Alice and Bob play optimally. Since this game satisfies the conditions of Zermelo's theorem, we can state with confidence that a player will win or lose given the position and that player’s method of play.

In the case of a single 1\times 1 grid, it's obvious that whichever player starts, loses. That's also true for any n\times n grid. We give the following definition: A position in the game has the value 0 if whichever player starts, loses.

For the case of a 1\times 2 grid, it's obvious that if Bob starts, he loses, but if Alice starts, she wins since there is one move available to her, after which the game goes to a position of two value-0 grids. In this case, we say the 1\times 2 grid has the value 1. Since adding a 2\times 1 grid to the game with a 1\times 2 grid "evens out" the game so that whoever starts by definition loses, we say the 2\times 1 grid has the value -1.

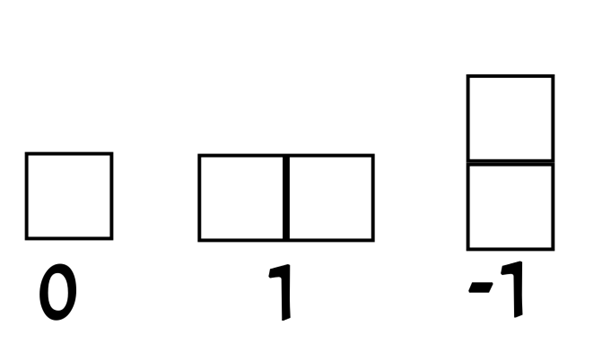
It can be verified that given a 2\times 8 grid, Alice wins whether she starts or not, and she still wins even if the game has two additional 2\times 1 grids. But if the game has three 2\times 1 grids, then the rule reverts back to whoever starts the game, loses. Since the value of each 2\times 1 grid is -1 and there are three of them, we say that the value of the 2\times 8 grid is 3.

In general, the value of an r\times c grid, denoted f(r,c), is

1. 0 if whoever starts the game loses.

2. n (for n\in\mathbb{N}) if after adding n 2\times 1 grids to the game, whoever starts the game loses.

3. -n (for n\in\mathbb{N}) if after adding n 1\times 2 grids to the game, whoever starts the game loses.

Your goal: Find the value of f(a,b) for

a = 4323855975562114726518487102722055842514310244656547479
b = 470147284842004245175081008799131351685318626829460321

A bonus "*" will be given for finding the value of f(a,b) for

a = 3396061787351437365560785267965234012799064104044242529256561027187645 

5409093065996282317126010161219412431254334813134471728518505247774471

40380830407565706177350759478762583119838528311717009



b = 7464746477226496222046301003339284704063450899406727072696371142567730

0099511708828335997683805844659240664138495004751184185917554576660019

30720494110499599758793660468148459835668058314279

We will post the names of those who submit a correct, original solution! If you don't want your name posted then please include such a statement in your submission!

We invite visitors to our website to submit an elegant solution. Send your submission to the ponder@il.ibm.com.

If you have any problems you think we might enjoy, please send them in. All replies should be sent to: ponder@il.ibm.com