September 2016
Motty Porat got a '*' as the only solution which proved optimality:
Dear Ponder,
Phew... This was something else!
But I'm thankful that 17 years after I learned that finite groups had interesting structures, something has finally forced me to delve into one.
Here is my solution, with only one violation, and a proof that there must be a violation.
CBACBADBCDABDCADBCDABDCA
BACDABCDABDCADBCDABDCABC
DCBADCBADCBACBDACBACDBAD
ADDBCDACBACDBACBADCBACDB
The process:
Let p[1]..p[24] be the ordering of the permutations. Since the permutations are a group, we can talk about their quotients r[1]..r[23] such that:
p[t+1] = p[t] * r[t]
p[t+2] = p[t] * r[t] * r[t+1]
In order to avoid violations, r[t], r[t+1], and r[t]*r[t+1] must be shuffles - permutations that move all elements.
There are nine shuffles, which are generated by three of them:
a = 3142 a^2 = 4321 a^3 = 2413
b = 4123 b^2 = 3412 b^3 = 2341
c = 4312 c^2 = 2143 c^3 = 3421
Notice that the order of a, b, and c is 4.
Looking at the multiplication table of the shuffles, we can see that:
- They generate the entire group of permutations.
- The products of two squares is the third one, e.g. a^2 * b^2 = c^2. (from the a,b,c above)
- Any other product of shuffles is not a shuffle, e.g. a*b = 2314; the 4 is at the 4th place.
As said, r[t], r[t+1], and r[t]*r[t+1] must be shuffles. Therefore r[t] and r[t+1] must be either:
(I) powers of the same generator, e.g. a^3 and a^2 => r[t]*r[t+1] = a^5 = a.
(II) squares, e.g. b^2 and a^2 => r[t]*r[t+1] = c^2.
- "The fundamental law of Ponder 9/16"
The series a^2, a, a^2, b^2, b, b^2, a^2, a, a^2, ... satisfies these requirements alternatively.
My solution is this series plus some improvisations at the ends. They include a violation (r[2] is not a shuffle), but luckily, both r[1]*r[2] and r[2]*r[3] are again shuffles, so the violation does not propagate to neighbors of neighbors!
The breakthrough:
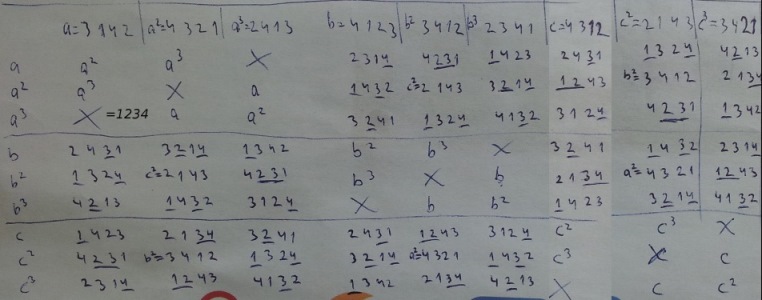
Since the squares (a^2, b^2, c^2) play an important role, let's check their effect on the other elements.
Let P = all 24 permutations;
Id = the unit element = 1234;
G = {Id, a^2, b^2, c^2} = {Id, a^2, b^2, a^2*b^2} = the subgroup of the squares.
The quotient group P/G comprises 6 cosets of 4 elements. I spared you their exact values.. For each x, multiplying x by the members of G (a^2, b^2, c^2) keeps it in the same coset, of course (xG), whereas multiplying x by a, b, or c jumps to a different coset in an orderly fashion:
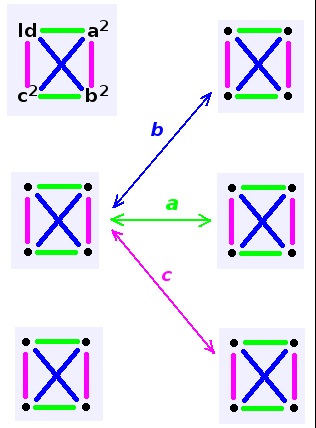
My solution:
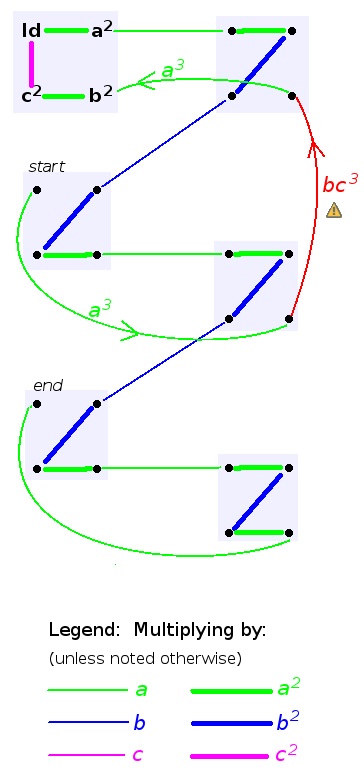
A proof that there must be a violation:
Back to the "fundamental law", let's divide the series of quotients (r[1]..r[23]) to sub-sequences with the same generator, e.g. [ a^2, a, a^2 ].
Each sub-sequence is at most 3 items long*, so there are at least 8 sub-sequences, and thus 7 joint-points. The joints are two squares, e.g. r[t] = a^2, r[t+1] = b^2. But then, p[t], p[t+1], and p[t+2] are all in the same coset. There are 6 cosets, so we can't visit them 7 times (and "burn" 3 elements each time) without duplication!
* If, for example, r[1], r[2], r[3], and r[4] were powers of a, then p[1], p[2], p[3], p[4], and p[5] would be p[1] times a power of a (including a^0). But there are only four different powers of a, and therefore one will repeat.