June 2022 - Challenge
Counting odd polyominoes
A polyomino is a generalization of dominoes and Tetris shapes: a connected set of cells on the 2D grid. Dominoes consist of two cells while Tetris shapes consist of four; a general polyomino has n cells.
We consider two polyominoes to be distinct even if they can be rotated/reflected into one another. In this approach, there are 2 distinct domino shapes and 19 distinct Tetris shapes:

It is easy to check that the sequence of the number of polyominoes of size n is 1, 2, 6, 19, 63, 216, 760, 2725, 9910, 36446, 135268,... (sometimes polyominoes counted this way are called fixed to differentiate from cases where symmetry is taken into account).
Since polyominoes are sets of 2D grid elements, we can associate a coordinate (a,b) with every cell, and we can use this to define order on cells. We define two such orders:
- ("left-right and then down-up"): (a,b) \le_1 (c,d) \Leftrightarrow a<c \vee (a=c \wedge b\le d)
- ("down-up and then right-left"): (a,b) \le_2 (c,d) \Leftrightarrow b<d \vee (b=d \wedge a\ge c)
For example:
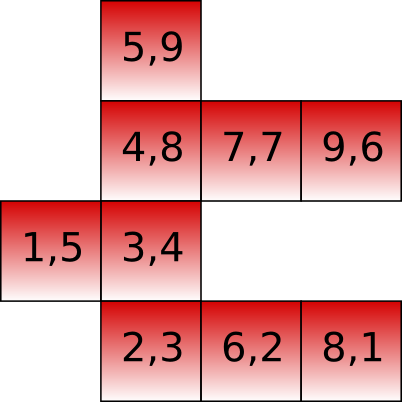
It is easy to see that \pi is a permutation. Recall that permutations can be either odd or even, according to the number of 2-cycles in a 2-cycle decomposition of the permutation.
If we count only polyominoes giving rise to odd permutations, we can see the resulting sequence starts with 0, 1, 3, 11, 35, 108, 380, 1348, 5014, 18223,....
Your goal: Find the above sequence of odd polyominoes up to n=18.
A bonus "*" will be given for finding the sequence up to n=20 (or even larger values of n - and tell me how you did it!).
We will post the names of those who submit a correct, original solution! If you don't want your name posted then please include such a statement in your submission!
We invite visitors to our website to submit an elegant solution. Send your submission to the ponder@il.ibm.com.
If you have any problems you think we might enjoy, please send them in. All replies should be sent to: ponder@il.ibm.com
Challenge:
01/06/2022 @ 11:30:00 AM EST
Solution:
04/07/2022 @ 12:00 PM EST
List Updated:
02/08/2022 @ 11:30 AM EST
People who answered correctly:
*Paul Revenant (1/6/2022 7:56 PM IDT)
*Bert Dobbelaere (2/6/2022 7:13 AM IDT)
*Gareth Ma (2/6/2022 12:21 PM IDT)
*Uoti Urpala (2/6/2022 4:18 PM IDT)
*Phil Proudman (2/6/2022 9:39 PM IDT)
*Sanandan Swaminathan (3/6/2022 6:05 AM IDT)
*Dominik Reichl (3/6/2022 3:36 PM IDT)
*Vladimir Volevich (4/6/2022 12:12 AM IDT)
*Anders Kaseorg (4/6/2022 9:32 AM IDT)
Gary M. Gerken (4/6/2022 3:03 PM IDT)
*Andreas Stiller (4/6/2022 5:27 PM IDT)
*Alper Halbutogullari (4/6/2022 7:55 PM IDT)
*David Greer (4/6/2022 11:32 PM IDT)
*Lawrence Au (5/6/2022 7:23 AM IDT)
*John Tromp (5/6/2022 9:49 AM IDT)
*Bertram Felgenhauer (6/6/2022 12:29 AM IDT)
Lorenz Reichel (7/6/2022 7:18 AM IDT)
Franciraldo Cavalcante (9/6/2022 11:30 PM IDT)
*Daniel Chong Jyh Tar (10/6/2022 2:44 AM IDT)
Balakrishnan V (10/6/2022 7:43 AM IDT)
*Harald Bögeholz (12/6/2022 4:57 AM IDT)
Daniel Bitin (12/6/2022 11:50 AM IDT)
Ali Gurel (12/6/2022 4:43 PM IDT)
*Latchezar Christov (13/6/2022 11:50 AM IDT)
Reda Kebbaj (13/6/2022 8:20 PM IDT)
Graham Hemsley (15/6/2022 9:31 AM IDT)
*Dieter Beckerle (15/6/2022 1:55 PM IDT)
Daniel Johnson-Chyzhykov (24/6/2022 3:32 AM IDT)
Tim Walters (25/6/2022 2:43 AM IDT)
*Nyles Heise (27/6/2022 5:06 AM IDT)
Marco Bellocchi (27/6/2022 9:20 PM IDT)
John Goh (28/6/2022 9:44 AM IDT)
*Antonio García Astudillo (28/6/2022 10:29 PM IDT)
*Karl Mahlburg (29/6/2022 1:47 PM IDT)
Michael Moffitt (30/6/2022 2:51 PM IDT)
*Andrew Milas (1/7/2022 9:50 AM IDT)
*Kang Jin Cho (1/7/2022 2:03 PM IDT)
FabioMichele Negroni (1/7/2022 6:08 PM IDT)
Todd Will (1/7/2022 8:26 PM IDT)
*Stéphane Higueret (2/7/2022 9:11 AM IDT)
Shouky Dan & Tamir Ganor (3/7/2022 8:30 AM IDT)
*Motty Porat (3/7/2022 11:54 PM IDT)
*Li Li (5/7/20228:39 PM IDT)