As we continue scaling up quantum processors, it’s becoming clear that we need more than just quantum volume to fully encapsulate the performance of utility-scale quantum computers. Therefore, we are debuting a new metric to benchmark our processors, called layer fidelity,1 and re-doing how we calculate CLOPS to sync with layer fidelity.
How are we benchmarking our quantum computers today?
Until now, we have been mainly benchmarking our processors using a quantity known as Quantum Volume.2 If a processor has a Quantum Volume of 2n, it means that the device is likely to produce the right output of a square quantum circuit on some subset of n qubits with n layers of random two-qubit gates. The Quantum Volume number is meant to represent the complexity of the computational space that the circuit can access. So, if eight of a processor’s qubits are stable enough to consistently return the correct values for a circuit with eight layers worth of gates, then the Quantum Volume is 28 or 256.
Quantum Volume is still the best way to make sure we do not game the systems for understanding crosstalk, errors, etc. But we always knew that we would need to find additional benchmarking metrics once we began releasing larger systems. For small volumes, Quantum Volume only samples a tiny part of the system. Quantum Volume spotlights a handful of the device’s best qubits, without talking holistically about the average performance across the system.
For large enough systems, Quantum Volume experiments will soon become too large for us to simulate classically — we won’t know whether or not our systems can pass the Quantum Volume test. Finally, Quantum Volume was designed to run on all-to-all connected systems, where every qubit can talk to every other qubit. In our 2D topology this means that every step up in Quantum Volume is taxing on the fidelity and the number of gates since we need to introduce many SWAP gates to move information around (each SWAP requiring three CNOT entangling gates).
Looking into the future, we need an additional metric that tracks continual improvements at 100+ qubits and that helps us understand the system’s ability to run large-scale, error-mitigated algorithms; a system can often return accurate error-mitigated expectation values for circuits with far more qubits or gates than its quantum volume would otherwise suggest. Ultimately Quantum Volume is still a very strong test of system performance, which we will continue to track. But as we are continually improving scale and quality then we need to augment our characterization portfolio with a new metric to benchmark against.
Introducing layer fidelity, a new quality metric
As we enter the age of quantum utility,3 we are introducing a metric that gives us a more granular understanding of our systems while accurately capturing the system’s ability to run the kinds of circuits that users are running today. We call this metric layer fidelity.
Layer fidelity provides a benchmark that encapsulates the entire processor’s ability to run circuits while revealing information about individual qubits, gates, and crosstalk. It expands on a well-established way to benchmark quantum computers, called randomized benchmarking. With randomized benchmarking, we add a set of randomized Clifford group gates (that’s the basic set of gates we use: X, Y, Z, H, SX, CNOT, ECR, CZ, etc.) to the circuit, then run an operation that we know, mathematically, should represent the inverse of the sequence of operations that precede it.
Layer fidelity provides a benchmark that encapsulates the entire processor’s ability to run circuits while revealing information about individual qubits, gates, and crosstalk.
If any of the qubits do not return to their original state by the inverse operation upon measurement, then we know there was an error. We extract a number from this experiment by repeating it multiple times with more and more random gates, plotting on a graph how the errors increase with more gates, fitting an exponential decay to the plot, and using that line to calculate a number between 0 and 1, called the fidelity.
So, layer fidelity gives us a way to combine randomized benchmarking data for larger circuits to tell us things about the whole processor and its subsets of qubits.
In order to extract the layer fidelity, we start with a connected set of qubits, like a chain of qubits where each one is entangled to their neighbor. Then, we split this connected set up into multiple layers so that each qubit only has at most one two-qubit gate acting on it — if you need a gate to entangle qubit one and qubit two, and another gate to entangle qubit two and qubit three, then these would be split out into two “disjoint layers.”
You can split them even further if you’d like. Then, we perform randomized benchmarking on each of these new disjoint layers to calculate the fidelity of each one. Finally, we multiply the fidelity from each layer together into a final number, the layer fidelity.
The value of layer fidelity
Layer fidelity is an extremely valuable benchmark. By running the protocol, we can qualify the overall device, while also having access to gate-level information, such as the average error for each gate in these layered circuits — the error-per-layered gate (EPLG) where EPLG=1-layer fidelity(1/[N-1]).
We can use it to approximate gammabar (γ̄), the metric we debuted last year to tell us about a specific device’s ability to return accurate error-mitigated results with the probabilistic error cancellation (PEC)4 protocol (γ̄=(1-EPLG)(-2)). Together with speed (β) we can use this to predict the PEC runtime γ̄{nd} * β. And most importantly, we already regularly benchmark the gate errors on our qubits; combined with the layer fidelity protocol, we can determine the best subset of qubits on the device. As part of our layer fidelity proposal, we ran 100-qubit layer fidelity on all of our 100 qubit devices, including our new 133-qubit 'Heron' processor. The results are shown in the Figure.
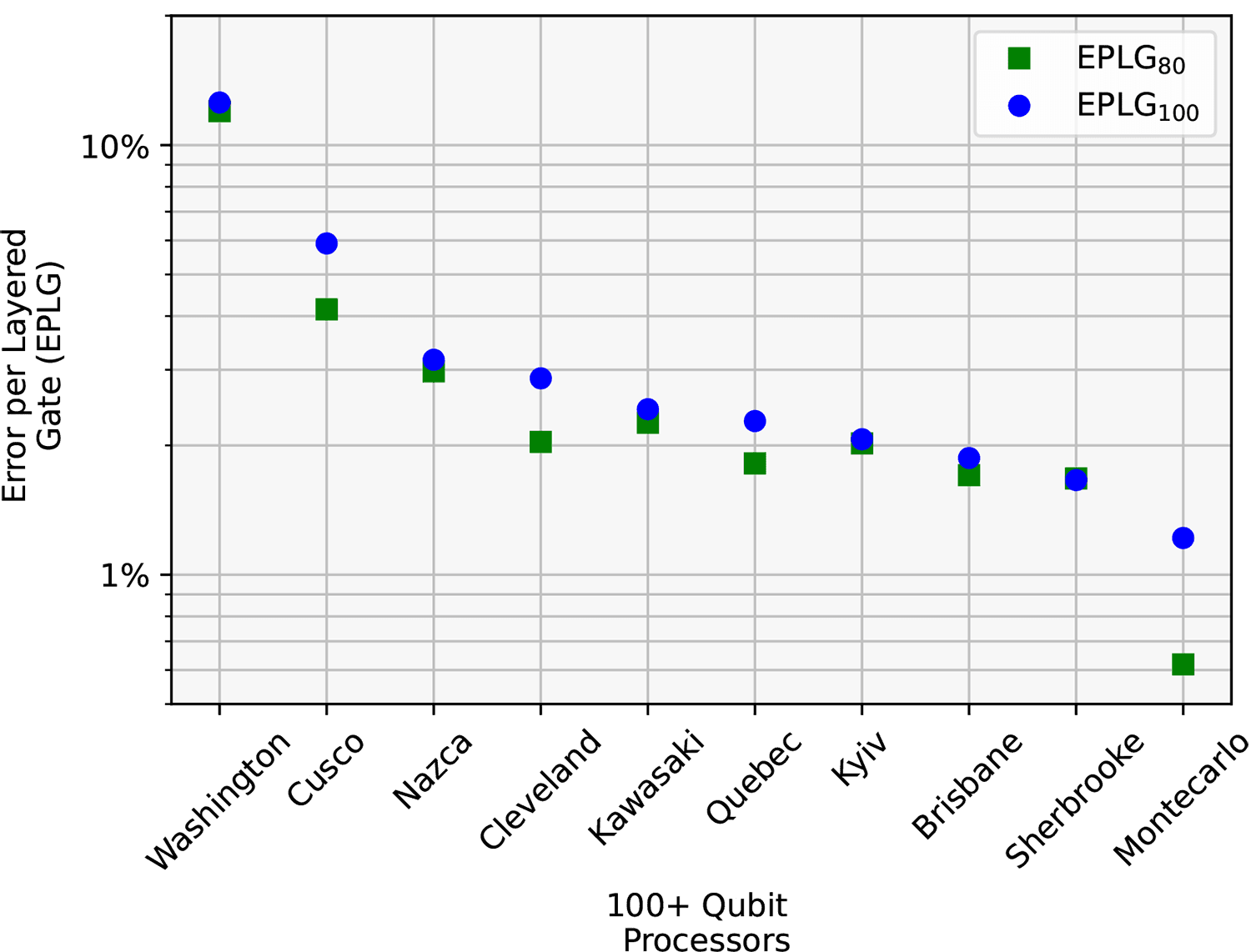
EPLG for 80-qubit and 100-qubit chains for our progression of 100+ qubit IBM devices, starting from Eagle R1 (ibm_washington), to Eagle R3 and, introducing our Heron R1 processor family with ibm_montecarlo. Soon, more Heron R1 devices will join this list.
How do we benchmark speed today?
Performance is the combination of quality, scale and speed. Since we are introducing a new quality/scale metric in layer fidelity, it’s an opportune time to update our speed metric, CLOPS,5 which stands for “circuit layer operations per second.” Crucially, CLOPS encapsulates both the time it takes to run circuits and the required real- and near-time classical compute.
Initially, CLOPS was conceived as a metric closely related to quantum volume. Each circuit layer is a Quantum Volume layer — a set of single qubit rotations plus a single set of random two-qubit gates. But CLOPS is a little more involved than that.
When we calculate CLOPS, we actually run 100 circuits in succession, where the outputs of the previous circuit inform the parameters of the following circuit. This means that our CLOPS measurement incorporates both the quantum (and real-time classical) computing needed to run circuits, and the near-time classical computing needed to update the values of subsequent circuits.
Or, in short: At present, CLOPS is a measure of how quickly our processors can run Quantum Volume circuits in series, acting as a measure of holistic system speed incorporating quantum and classical computing.
Introducing an updated CLOPS
But there’s a catch to this. The way we think of Quantum Volume layers is more or less idealized.
A single-qubit rotation, plus random two-qubit gates that we program in Qiskit requires more gates to actually carry out in hardware after we’ve compiled a circuit to a language the quantum processor can actually understand. The realities of our physical processors — especially how their qubits are connected — means that what we consider a “layer” theoretically may require multiple layers to implement on the machine. Or in short, we’ve been calculating CLOPS assuming this idealized version of how circuits run, rather than with a hardware-aware technique.
Therefore, we’re updating CLOPS to better reflect how our hardware really runs circuits.
Our updated CLOPS metric, called CLOPSh is simply accounting for how hardware really runs. CLOPSh defines a “layer” differently. Rather than a layer representing a set of two-qubit gates acting across all random pairs of qubits at once, now a layer only includes the two-qubit gates that can be run in parallel on the system architecture. Basically, if a Quantum Volume layer previously had two gates that couldn’t be run in parallel on the hardware architecture, we’d have to break that up into two or more layers in our updated CLOPSh calculation.
Similar to layer fidelity, CLOPSh allows us to calculate our hardware capabilities in a way that’s truer to the way that the hardware operates. Before, CLOPS was too specific to the hardware; two different processors might compile gates differently or have different abilities to run gates in parallel, and therefore their CLOPS values would differ without necessarily representing true differences in performance.
But with a hardware-efficient CLOPSh, we can now compare apples to apples with a more universal definition of a circuit layer. CLOPSh is also directly related to β (β = 1 / CLOPSh), so improvements in CLOPSh will directly apply to improvements in runtime of PEC and similar error mitigation techniques.
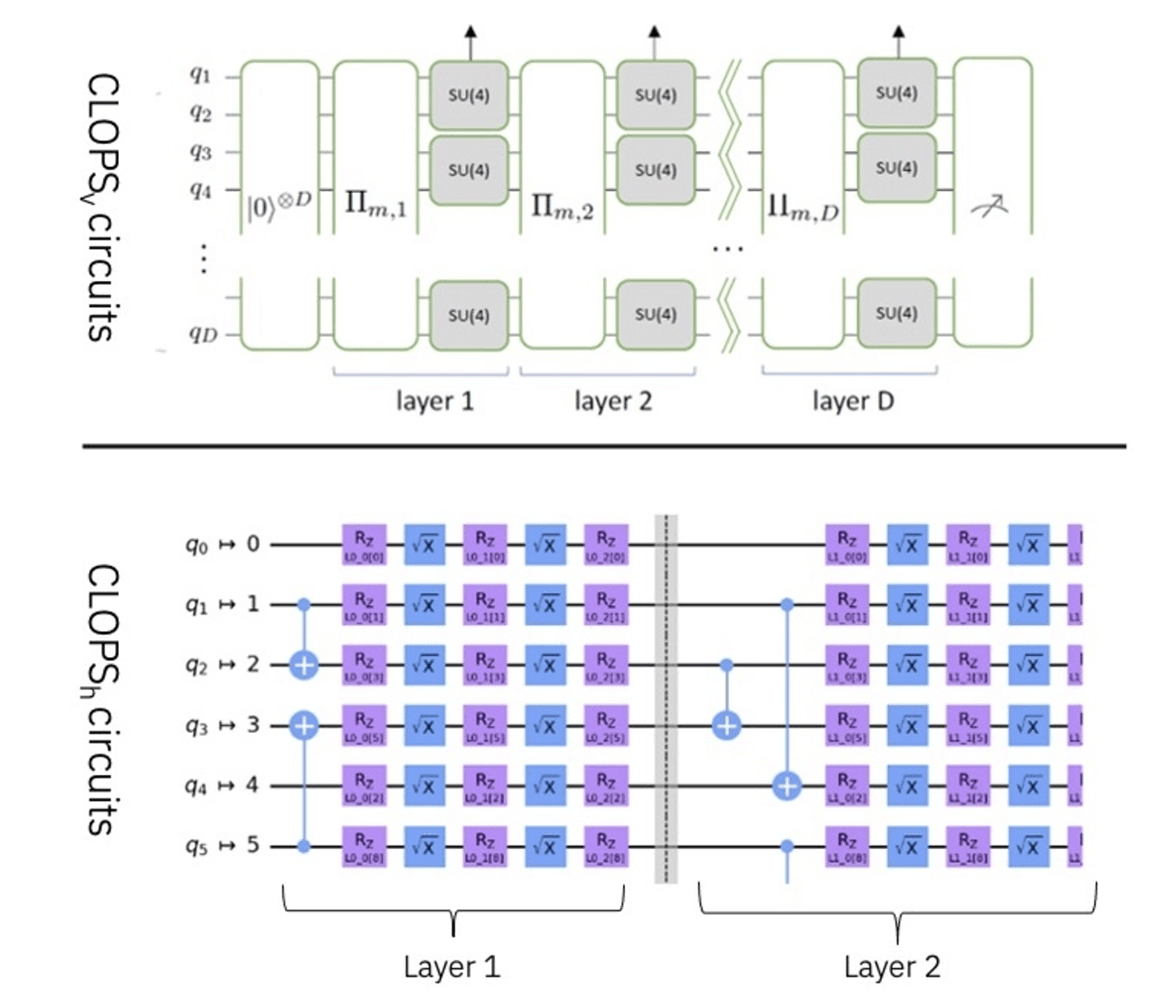
We used to calculate CLOPS with Quantum Volume circuits, which are virtual circuits, without regard to device connectivity (top). Now, we’re calculating CLOPS in a hardware-aware way (bottom).
This is also important in the era of 100x100 — remember, we promised to deliver accurate expectation values for 100-qubit, 100-layer circuits by the end of next year — since this is how we calculate layers. Additionally, we can now measure the capabilities of the software stack to efficiently run large utility scale circuits which requires significant engineering effort.
In 2024, we intend to offer a tool capable of calculating unbiased observables of circuits with 100 qubits and depth-100 gate operations in a reasonable runtime.
Together, layer fidelity and CLOPSh provide a new way to benchmark our systems that’s more meaningful to the people trying to improve and use our hardware. Therefore, going forward, these metrics are being displayed on the system property cards for our 100+ qubit devices, which are found on our IBM Quantum systems resources. These metrics will make it easier to compare systems to one another, to compare our systems to other architectures, and to reflect performance gains across scales. And ultimately, these metrics will help us continue pushing our performance so that users can run 100+ qubit circuits on our systems in this era of quantum utility.
