Doubling the Size of Quantum Simulators by Entanglement Forging, published in PRX Quantum, introduces a new method of quantum simulation called entanglement forging, which enables researchers to simulate a given quantum system using only half as many qubits on a quantum computer.
We’ve come a long way in terms of our ability to model complex physical systems on quantum hardware, and it seems that each year brings both powerful new tools and remarkable achievements in the field of quantum simulation. But despite all that progress, today’s quantum computers are still too small and noisy to exhibit full quantum advantage.
A team of IBM researchers has been looking for a new way to give quantum simulation technology a boost, but their goal isn’t to enhance the hardware, itself. Instead, they’re developing new techniques for combining quantum and classical computing resources to tackle simulation problems that are too hard for today's noisy quantum hardware. The results of these efforts could represent a major step forward in the quest towards quantum advantage.
This isn’t the first time that researchers have thought to incorporate classical computing resources in quantum simulation. In fact, classical computing powers many techniques that are widely used in quantum simulation today, including variational quantum eigensolver (VQE) methods and error mitigation. Now, with a newly published paper1 in PRX Quantum, the IBM team has introduced a new method of quantum simulation called entanglement forging, which enables researchers to simulate a given quantum system using only half as many qubits on a quantum computer.
In their paper, the IBM team demonstrate this by using entanglement forging to create a remarkably accurate simulation of the ground state energy of a water molecule, successfully representing 10 spin-orbitals on just five qubits of IBM’s 27-qubit Falcon quantum processor. Given its scalability and broad application across a variety of problem structures, entanglement forging could markedly expand the computational power of quantum systems, especially when combined with new programming models like IBM Quantum’s quantum serverless — a new programming model that takes advantage of quantum and classical resources.
Under most circumstances, if researchers wanted to simulate 10 spin-orbitals of a water molecule, they would need to do so using a quantum computer with at least 10 qubits. That’s because most quantum simulation techniques require one qubit for each relevant “feature” of the systems they simulate. With entanglement forging, IBM Quantum researchers were able to effectively split the problem in half. This means they separated the 10 spin-orbitals into two groups of five, and then processed each grouping using just five qubits.
“We demonstrated a method that in many cases will allow you to run larger problems on your quantum processor than you otherwise could,” said Andrew Eddins, IBM Quantum researcher and lead author on the recent paper. “Entanglement forging provides an efficient method of bringing classical computational resources to bear on quantum problems in a way that, in one respect, doubles your capability. It effectively increases your qubit number by a factor of two, which is really remarkable.”
Exploiting problem structures to increase the power of quantum computation
According to Sarah Sheldon, an IBM Quantum research staff member and co-author on the paper, entanglement forging represents an important addition to a well-established family of quantum computational techniques known as “circuit knitting.”
“There’s a bit of an evolution here,” Sheldon said. "Other groups have worked on similar ideas of breaking up circuits into smaller pieces, either by qubits or in time — like breaking up gates — to do larger problems. Entanglement forging is a particularly scalable method, at least for problems with weak entanglement that have this structure that’s amenable to it."
Indeed, the structure of a system or problem plays a crucial role in enabling the entanglement forging technique, which essentially works by dividing systems into two weakly entangled halves, modeling those halves separately on a quantum computer (i.e. first one half, then the other), and then using classical resources to calculate the entanglement between them.
Entanglement forging enables researchers to simulate a given quantum system using only half as many qubits on a quantum computer.
Here, the phrase “weak entanglement” simply indicates that there are relatively few correlations between the two halves of the original system. This makes entanglement forging a natural fit for the task of modeling molecular systems in cases where there is limited entanglement between the spin-up and spin-down orbitals.
However, according to Eddins and Sheldon, the usefulness of entanglement forging could extend far beyond chemistry simulations. “It isn’t at all restricted to the chemistry setting that we focus on in the paper — to VQE problems, to molecular Hamiltonians, etc.,” Sheldon said.
“There may be other systems — for example, spatial partitions in lattice models — where there is a natural partition that you can use to easily divide the system into two weakly entangled halves. You can also apply entanglement forging to systems that aren’t weakly entangled. We just have to do more computation on the classical computer either to determine how best to partition the system, or to represent the correlation between the two halves.”
How entanglement forging works
To understand why entanglement forging may be useful for quantum simulation, it’s helpful to see how it works, step-by-step.
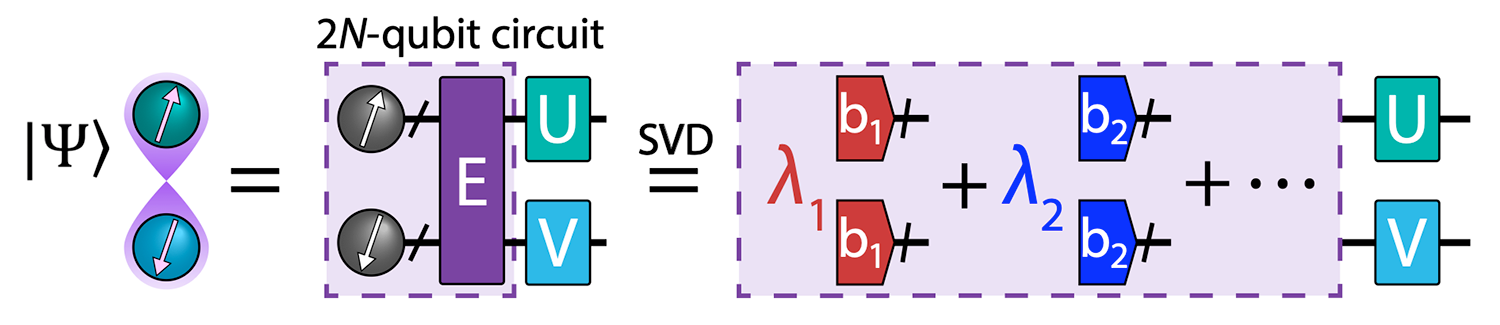
In the first section of the three-part figure shown, for the molecular system of H2O (or other weakly entangled molecules), the two divided halves will correspond to the spin-up and spin-down parts of the molecule — labeled using arrows pointing in the appropriate direction.
To start, let’s say we want to simulate some quantum state called psi (in this case, the state of a molecular system like water), prepare that state on a quantum computer, and then perform measurements to learn some property of the state — i.e., to measure an observable of the state such as its energy. We divide this state into its two natural halves, which may share some entanglement.
For the molecular system of H2O (or other weakly entangled molecules), the two halves we divide it into will correspond to the spin-up and spin-down parts of the molecule. As such, we label those two halves using arrows pointing in the appropriate direction. All of this is illustrated in the first section of the three-part figure shown above.
Entanglement forging takes a generic circuit that operates on the combined system of the spin-up and spin-down halves, and splits it into smaller circuits that only operate on one half at a time. In other words, the entanglement forging technique takes a circuit operating on 2N qubits, and separates that circuit into two N-qubit halves. (For reference, see the section of the figure shown above labeled “2N-qubit circuit.”)
From there, researchers then combine the outcomes of these circuits into a summation that is weighted by a list of values that determine the entanglement structure of the original system, i.e., the correlations between the two halves. This is where classical computational resources enter the picture. The classical computer takes care of representing the entanglement structure between the two halves by keeping track of the aforementioned list of values, and those values then determine the smaller experiments the quantum computer must run to learn properties of the entire state.
Weak entanglement leads to scalability
Entanglement forging may lighten a quantum computer’s load a great deal when it comes to representing the entanglement between two halves of a given system, but it still comes with its own set of potentially significant computational costs, particularly on the classical side. The classical computer must maintain the list of values that represents the entanglement structure, and that list can get very large. The classical computer uses that list to tell the quantum computer which states it needs to prepare and measure to compute terms in the summation. The summation gives us the total energy of the system.
Moreover, there can be a large overhead cost in the number of these measurements that must be taken. However, if the entanglement is weak, the summation will be nearly equal to just the first few terms, and the rest of the terms will be comparatively small. This is helpful because, in practice, we can focus on the leading terms, substantially reducing our overhead cost.
To demonstrate their technique, the researchers ran a unique version of a traditional VQE experiment simulating a 10 spin-orbital model of the water molecule using just five qubits. Normally, modeling the spin-up and spin-down electrons in each orbital would require 10 qubits, but with entanglement forging, the researchers were able to simply run the two halves of the molecular system separately.
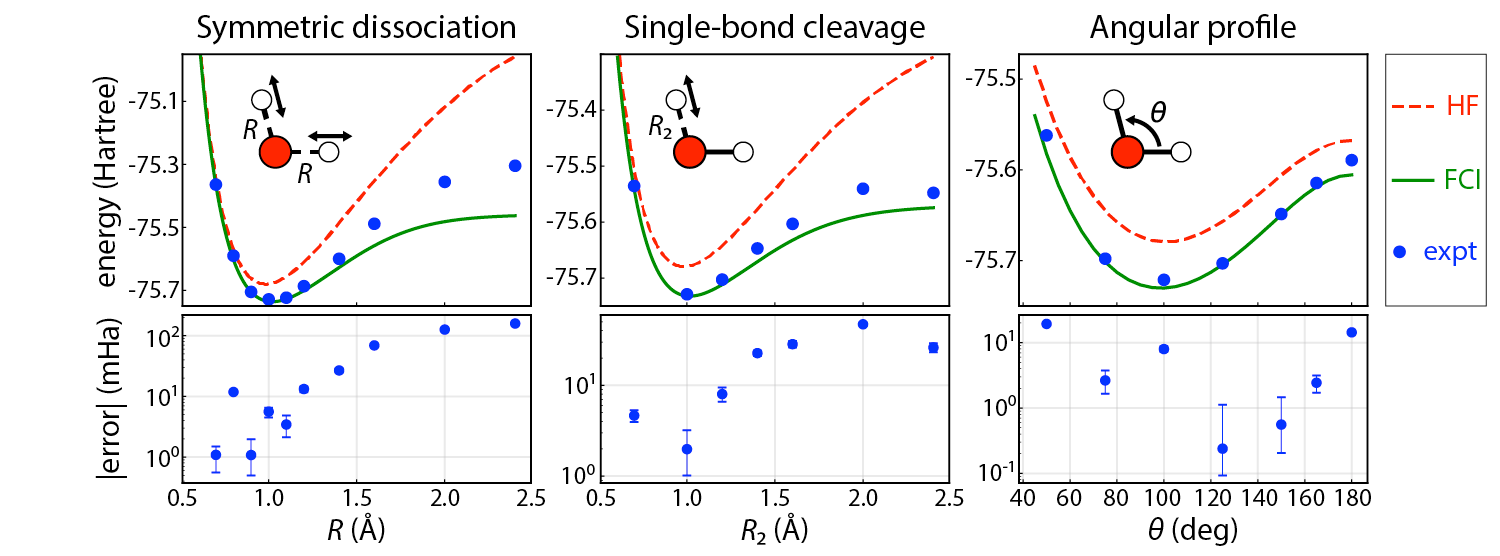
Repeating the experiment for a range of molecular geometries, as indicated, the research shows that entanglement forging generated highly accurate results on the order of 1-10 millihartree.
Ultimately, the researchers were able to calculate the energy of the full 10-qubit system, even though they were only using five qubits. Repeating the experiment for a range of molecular geometries, as indicated in the figure above, the researchers showed that the technique generated highly accurate results on the order of 1-10 millihartree in the near-equilibrium region of primary interest.
Interested in experimenting with entanglement forging yourself? Keep an eye on the IBM Research blog, where the IBM Quantum team will soon debut a software package that enables users to reproduce key results published in PRX Quantum and apply the capability to their own work.
Entanglement forging, quantum serverless, and the future of quantum technology
IBM Quantum platform lead Blake Johnson says entanglement forging could have profound implications for near-term quantum technology. “Entanglement forging essentially enables you to cut up a larger circuit into smaller circuits that we can execute on smaller hardware,” he said. “Smaller circuits aren’t just easier to execute. They’re also able to tolerate a lot more noise just by virtue of being smaller.”
Johnson also noted that the small circuits and the high accuracy associated with the technique make for a powerful complement to IBM’s quantum serverless model, where developers can make use of QPU, CPU, and GPU resources without needing to consider infrastructure management. The serverless programming model allows users to more easily program in a unified, cross-platform environment — making it easier than ever for users to combine both quantum and classical computing in their programs. This is especially true when considering how circuit knitting may be used in cases outside of molecular simulation, where determining how best to divide a system into two weakly entangled halves may not be so obvious.
“In general, if you want to expand entanglement forging to a broader set of problems, a potential workflow might involve a step in the process where you are searching for the best places to cut, where reassembly will be least costly,” he said. If researchers don’t know the best places to cut ahead of time, they’ll likely need to use classical computational methods to evaluate various cuts for the expected cost of reassembly, as well as computational resources that can perform reassembly in the cases where it isn’t cheap.
“That’s the sense in which entanglement forging and other circuit knitting techniques may need something like our serverless concept,” he said. “Serverless provides powerful classical resources for performing the reassembly or the analysis of the most advantageous places to cut.”
At the same time, Johnson sees techniques like entanglement forging playing a vital role in pushing the capabilities of near-term quantum computers as far as they can go.
“We need entanglement forging and techniques like it to do accurate calculation of circuits that are at the threshold or even beyond the threshold of what we can do today, and to extend the computational power of our quantum systems. Techniques like this may put quantum advantage within reach of upcoming generations for quantum hardware.”
Robert Davis is a technical writer for IBM Quantum.
