Read more about the announcements made at the 2022 IBM Quantum Summit:
Dynamic circuits are a powerful capability that open new avenues to achieving quantum advantage in the near term. By seamlessly incorporating real-time classical communication into quantum circuits, this feature will greatly increase the variety of circuits that one can run on near-term quantum hardware, while providing a way to run workloads with a fraction of the gates. We expect dynamic circuits to form an important part of many quantum applications in the future.
So, what are dynamic circuits? A quantum circuit is a sequence of quantum operations — including gates, measurements, and resets — acting on qubits. In static circuits, none of those operations depend on data produced at run time. For example, static circuits might only contain measurement operations at the end of the circuit. Dynamic circuits, on the other hand, incorporate classical processing within the coherence time of the qubits. This means that dynamic circuits can make use of mid-circuit measurements and perform feed-forward operations, using the values produced by measurements to determine what gates to apply next.
In a mathematical sense and absent experimental constraints, static and dynamic circuits have the same computational power. That is, any problem representable with a dynamic circuit can also be represented as a static one. However, dynamic circuits can assist in overcoming some of the limitations of real hardware. In particular, dynamic circuits offer new opportunities to trade off circuit depth and width, which can be the difference between a circuit which works and one whose output is indistinguishable from noise.
Exploring the power of dynamic circuits
The quantum research community has already identified a number of applications of dynamic circuits. These examples span quantum error correction, quantum simulation, quantum machine learning applications, and much more.
Take error correction as an example. Error correction requires us to encode quantum information across many physical qubits, and then repeatedly perform so-called syndrome measurements in order to detect the presence of errors. Real-time classical decoders identify error locations from the syndrome data. One major challenge of realizing error correction is performing logical gates on the error-corrected processor. Two popular methods of realizing these gates, called gate teleportation and gauge fixing, both require mid-circuit measurements with feed-forward from the decoder to realize.
Dynamic circuits are also provably better than static circuits when it comes to preparing certain highly entangled quantum states for quantum simulation, such as those states describing topological quantum order and quantum phase transitions. For topological quantum order, we simulate a lattice of quantum spins that interact with nearby spins. If we cool that system down to very low temperature, they organize themselves into a highly-entangled state. Without dynamic circuits, performing this simulation would scale linearly with the lattice size; doubling the size of the lattice means doubling the size of the corresponding circuit. But with dynamic circuits, the corresponding circuit almost doesn’t grow as the lattice increases in size. This can provide an exponential speedup in terms of circuit depth.
Dynamic circuits are also provably better than static circuits when it comes to preparing certain highly entangled quantum states for quantum simulation.
Once we’ve prepared these topological quantum order simulations, we can study them with quantum machine learning to understand which quantum phase they belong to, where a quantum phase is much like a quantum version of matter phases like solids, liquids, or gases.
Recently, a team led by Mikhail Lukin’s group at Harvard devised a quantum neural network1 that could perform this classification analysis. A quantum neural network is a circuit that alternates between two kinds of gate layers: the first performs the convolution step, filtering so only important information remains, and a pooling step, which intensifies that information. Performing these steps require measurement and feed-forward as we switch between layers as we sort the states into their phases.
These are just three examples — examples which only scratch the surface of the potential capabilities that dynamic circuits can give to our users.
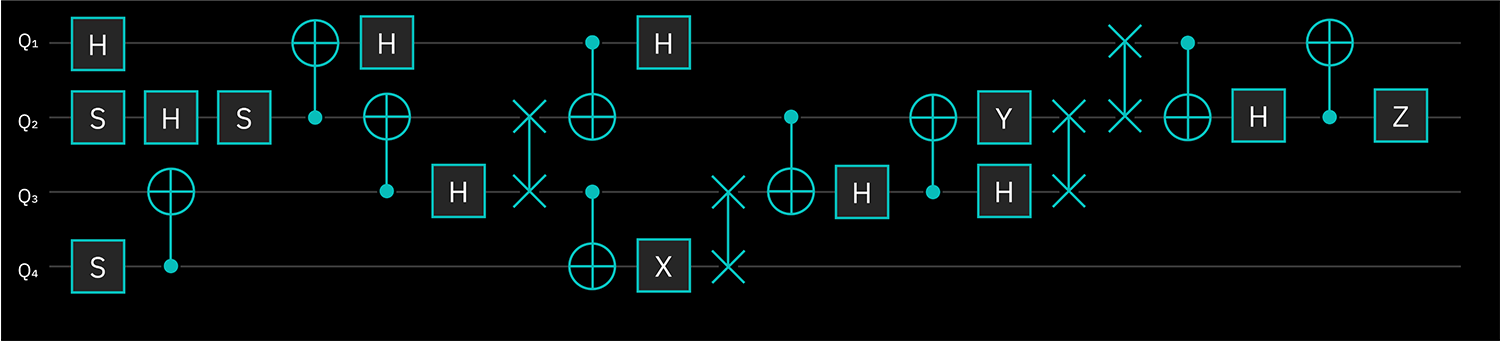
Before: A quantum circuit.
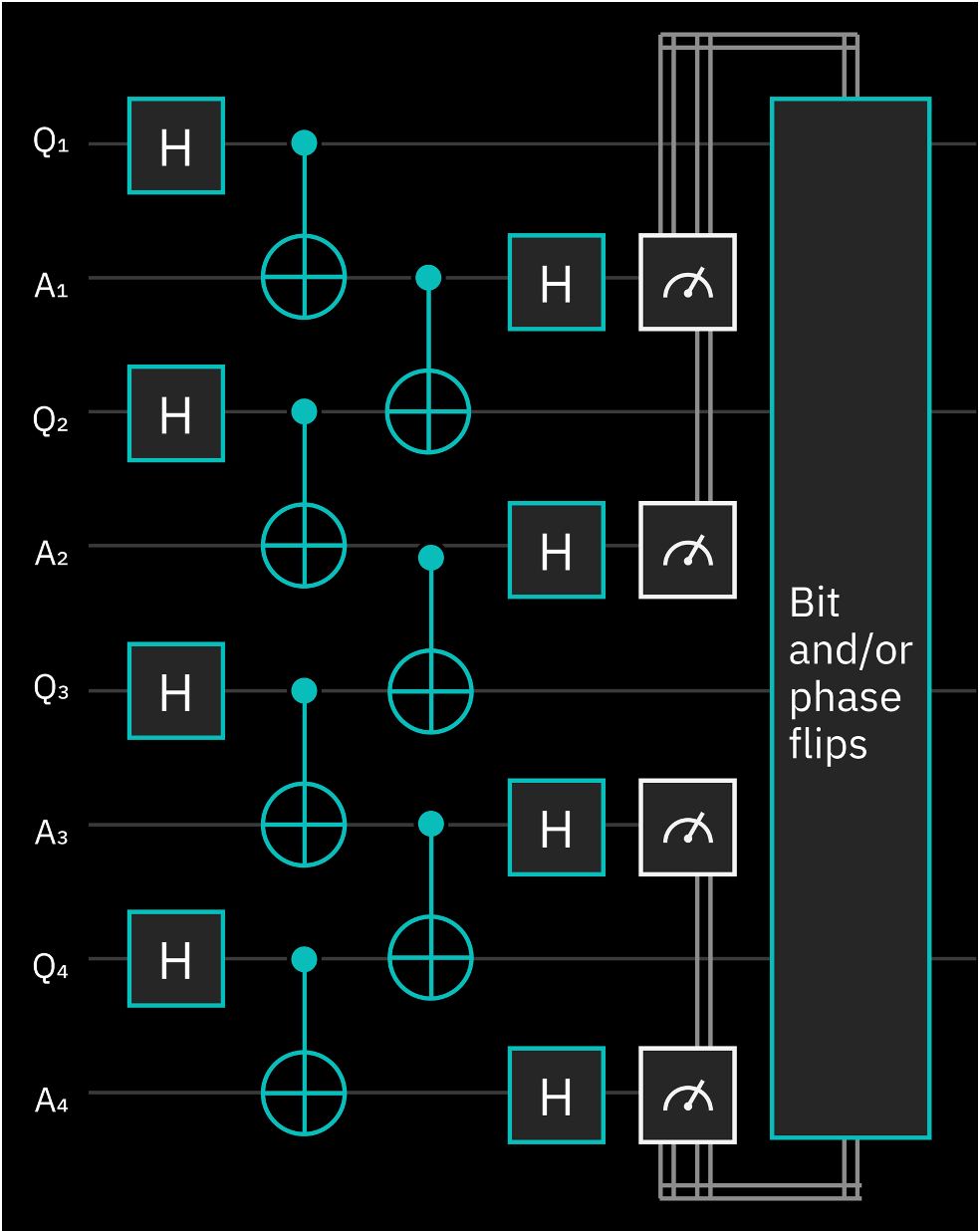
After: A dynamic quantum circuit.
Bringing dynamic circuits to IBM Quantum hardware
At IBM, we have been exploring dynamic circuits for several years. Recently, we compared the performance of static and dynamic circuits
Quantum circuits get a dynamic upgrade with the help of concurrent classical computation. Read more.
To make this capability more broadly accessible has required enormous effort. We had to rebuild a substantial portion of our underlying infrastructure, such as re-architecting our control hardware such that we could move data around in real time. We needed to update OpenQASM so it could describe circuits with feed-forward and feed-backward control flow. And we had to re-engineer our compilation toolchain so that we could convert these circuits into something our systems could actually run.
Now, in 2022, we are rolling out dynamic circuits on 18 IBM Quantum systems — those QPUs engineered for fast readout. Users can create these circuits using Qiskit or directly in OpenQASM3. They can execute either form through the backend.run() interface. We expect that early next year, we’ll be able to execute payloads with dynamic circuits in the Sampler and Estimator primitives in the Qiskit Runtime, too.
Ultimately, dynamic circuits are part of our broader push to bring about the next wave in high-performance computing: quantum-centric supercomputing. As we progress along our development roadmap, we’re designing modular quantum processors that are extensible with either quantum or classical links. Our team has been exploring ways to execute large quantum circuits across several smaller processors by splitting them into smaller circuits to run in parallel. This technique comes with a cost, though: an overhead that scales like O(9n), where ‘n’ is the number of gates that we cut. However, with dynamic circuits spanning multiple QPUs, we can reduce that overhead to O(4n).
We call this execution model local operations with classical communication, or LOCC.
Dynamic circuits aren’t just an nifty new tool for today’s processors, but part of our broader mission to bring about useful quantum computing. We hope you’ll try them out today.
Explore executing circuits with feedback and feed-forward operations to extend what is possible with quantum circuits. Read about building dynamic circuits and try some tutorials.




