In the Nature Physics paper, “Quantum advantage for computations with limited space,” IBM Quantum scientists prove mathematically that there are functions that the restricted classical computer cannot compute but that the restricted quantum computer can.
Quantum computers will, we hope, soon offer advantages over today's classical computers when it comes to tackling certain important problems. But quantum computers won't beat their classical counterparts based simply on the fact that their underlying architecture is different. We must find and write theoretical proofs of these advantages, and then demonstrate them experimentally. Here, for the first time that we are aware of, we report a simultaneous proof and experimental verification of a new kind of quantum advantage. Specifically, we show that qubits, even today's noisy qubits, offer more value than bits as a medium of storage during computations.
Our team thinks of computing in terms of circuits. At the start of a circuit, we have a number of classical or quantum bits, like swimmers in swim lanes. We set these bits to an initial value, and then the circuit progresses forward through a user-written program, consisting of gates. Different gates have different effects on these bits. The output of such a circuit is a set of zeroes and ones in both the classical and quantum case.
In the classical version, these bits are switches that can only take one of two positions—on or off—and can interact inside gates that flip switches based on the inputs to this gate. Quantum bits, however, have access to a larger space of values; they can take on a combination of the two switch positions each with a corresponding amplitude, represented by a complex number. Quantum gates create states incorporating every possible combination of switch positions, and combinations of gates can increase or decrease the amplitudes across a state spanning many qubits. Upon measurement, each qubit returns a single classical bit, with the amplitudes dictating the probability of returning each qubit value.
In our work, “Quantum advantage for computations with limited space,”1 published today in Nature Physics, we explored what we call the limited space computations. These are circuits restricted to using two-input gates, and limited to using one bit of computational/scrap space. This restriction allows us to establish a fair comparison between the power of classical and quantum computational space, and in particular demonstrate a fundamental advantage of computing with qubits over classical bits.
Through our research, we're exploring a very simple question: how does the computational power differ when a computer has access to classical scratch space versus quantum scratch space?
In our paper, we prove mathematically that there are functions that the restricted classical computer cannot compute but that the restricted quantum computer can.
We didn't stop at theoretical proofs for this paper, though—we also pitted a real (albeit noisy) quantum computer against a classical computer. Our demonstration includes the study of the simplest function that cannot be computed classically in the one-bit limited space model: finding the majority of three bits (that is, returning zero if more than half of the bits are zero, and returning one if more than half of the bits are one).
We armed the limited classical computer with access to random Boolean gates to further increase its computational capabilities. But even with access to this randomness, the classical computer can only succeed 87.5 percent of the time whereas a perfect, noiseless quantum computer could succeed 100 percent of the time.
Of course, real quantum computers today are noisy, which degrades the success probability. To combat this, we calibrated special entangling gates—fractional CNOT gates—in order to perform these circuits more efficiently. Using this technique, our limited-space quantum computer demonstrated a success rate of 93 percent, still beating the limited-space classical computer. This result demonstrates that a noisy quantum computer with as few as four qubits (three input qubits to encode the input; one qubit to use as computational or scrap space) can perform calculations inaccessible to a perfect classical computer.
The controlled-NOT gate, also known as the controlled-x (CX) gate, acts on a pair of qubits, with one acting as ‘control’ and the other as ‘target.’ It performs a NOT on the target whenever the control is in state ∣1⟩. If the control qubit is in a superposition, this gate creates entanglement.
But we didn't stop there. Quantum computers also face the challenge of limited qubit connectivity. In the three-input, one-computational qubit case, each input qubit can interact directly with the computational qubit. However, when we expand the problem to more input qubits (four, five, and six inputs), not all inputs can interact directly with the computational qubit due to the topology of our quantum hardware—how the qubits connect to one another. Therefore, in practice we must implement costly SWAP operations in order to execute these circuits.
The SWAP gate swaps the states of two qubits.
While our publication shows that the quantum computer can still outperform the classical computer with larger numbers of inputs despite having to implement the SWAP gates, we can leverage a new hardware capability, mid-circuit reset, to further improve the performance of circuits. Now, instead of SWAP-ing qubits to interact them with the computational qubit, we can reset the physical qubits that are adjacent to the computational qubit and re-initialize them to a new qubit state. With high fidelity mid-circuit reset, we show an improvement of 3 percent over the SWAP circuits.
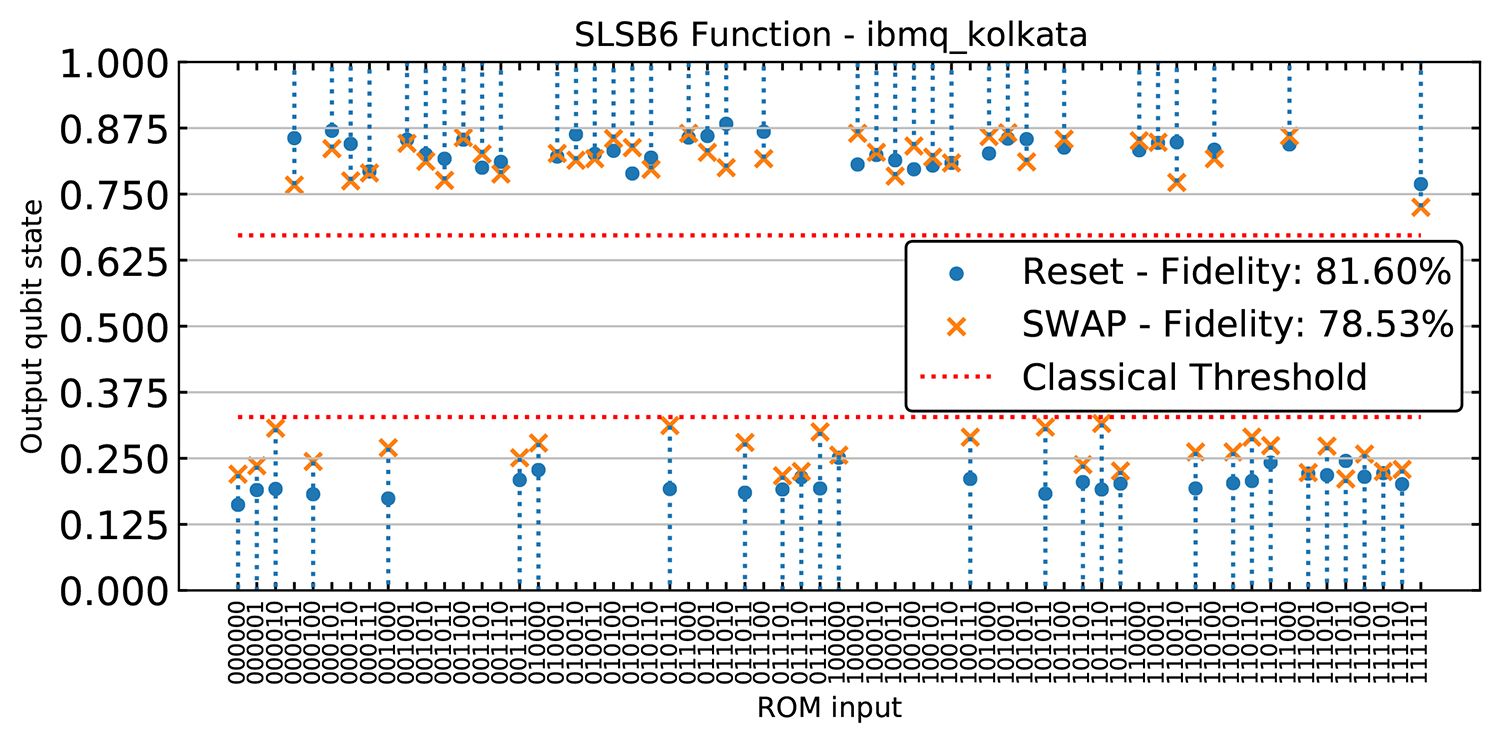
The output state of the computational qubit for every possible input qubit combination for the six input “Second Least Significant Bit” (SLSB) function. The dotted blue lines indicate the correct output (one or zero) for each input while the horizontal dashed red lines indicate the average success rate for a one-bit classical computer. Outputs achieved by the quantum computer outside the red lines thus indicate a quantum advantage. The data points shown indicate that the mid-circuit reset (blue dots) improves the performance of the circuit compared to the SWAP circuit (orange Xs).
Breaking Holevo's boundary
This is result has important implication—it shows that quantum computers, even noisy quantum computers, are powerful computational tools. This result seems to “break” a well-known boundary set by physicist Alexander Holevo—we know from Holevo's work that one qubit can only store one bit of information, but our paper demonstrates that you can store much more than one bit as the intermediate results of a computation.
At an even deeper level, demonstrating that quantum systems do things that classical physics cannot explain has long been a fundamental part of the study of quantum information science. Most famously, physicist John Stewart Bell showed that the classical rules of physics and probability fail to explain the behavior of correlated particles obeying the rules of quantum mechanics, even if the particles are too far away to communicate.
Our team continued the legacy of Bell with similar-spirited tests of our own. Prior to this work, we explored what happened if we limited the depth of computation, but not the available bits. We proved that not only do perfect quantum computers give an advantage over classical computers on these “shallow circuits,” but even noisy quantum computers do. Taken together, our work shows how quantum computers compare to classical computers in terms of both computational time and space.
The IBM Quantum team is continuing to develop hardware that we hope will provide speedups for some of today's hardest quantum computing problems, as well as improvements to the variety of operations accessible to quantum computations in order to maximize the performance of that hardware. Amid this development, the theory team will continue to carry out equally important work: investigating and demonstrating the uniqueness of quantum computation, and what kinds of benefits over classical computers such uniqueness may deliver.
