Usually, when we want to simulate a quantum state using quantum circuits, we prepare some initial state and use unitary operators—quantum logic gates—to evolve it over time. Once we reach the end of the circuit, we take measurements that collapse the quantum state into a classical one, yielding the information we sought to glean from our simulation. Or at least that's one way of doing things.
Increasingly, researchers are investigating quantum algorithms that use the act of measurement itself not only to extract information from quantum states, but also to steer and manipulate them as they evolve in time. This can be particularly helpful when it comes to generating entanglement, an essential task in quantum information processing. Entanglement generation in purely unitary circuits often leads to high-depth circuits that are beyond the capabilities of today’s hardware. Quantum circuits that incorporate measurement—for example, dynamic circuits that allow us to perform logical operations in our circuits based on mid-circuit measurements—can be much more efficient.
In recent blog posts, we’ve seen dynamic circuits enable efficient measurement-based methods for entangling disconnected qubits in a superconducting quantum processor, and even for entangling qubits on separate processors. A paper published in Nature Physics highlights more of the many capabilities measurement-based quantum protocols can enable, underscoring their potential to support progress in fields like condensed-matter physics and quantum error correction.
In that paper, researchers from IBM, University of Cologne, and Harvard demonstrate an efficient measurement-based protocol for generating a simple long-range ordered state—i.e., a quantum state in which long-range entanglements are maintained across significant distances within the system. Crucially, we were able to achieve this at the utility scale, using as many as 125 qubits on an IBM Quantum™ Eagle processor to build long-range order across up to 54 qubits.
By tuning both coherent and incoherent error rates in their quantum circuit, we show that it is possible to maintain this long-range order in two spatial dimensions up to a critical point known as the Nishimori transition. We then use a classical decoder to ascertain the signature of the long-range ordered state. Prior to this experiment, it was not known whether it was actually possible to create and validate this kind of long-range order in a quantum circuit given the presence of measurement error.
Below, we’ll dive into the details of the experiment and show how the protocols we developed alongside our collaborators at University of Cologne and Harvard could significantly enhance quantum simulations of different phases of matter relevant to condensed-matter physics and other fields of physics research. We’ll also discuss how these new methods help to reveal fascinating insights into the nature of quantum information itself.
Interested in realizing a Nishimori phase transition on your own? Recreate the experiment with an IBM Quantum processor by following our tutorial on IBM Quantum Learning.
Exploring phase transition with quantum circuits
In our experiments, we set out to simulate the “phase transition” of a disordered quantum state evolving into a long-range ordered state. In particular, we set our sights on realizing the Greenberger-Horne-Zeilinger (GHZ) state—the simplest example of long-range order in quantum systems, and one of the few large-scale entangled quantum states that have been well-studied. You can also think of the GHZ state as the ground state of the random bond Ising model, a simplified model of magnetism that is used widely in physics research and which served as the model of interest in the 2023 IBM Quantum utility experiment.
We should note that the utility experiment concerned the transverse-field Ising model where spins interact with a magnetic field that is perpendicular to the spins’ alignment. This experiment, on the other hand, centers on the random bond Ising model, where the spin system tends to exist in a disordered state due to variations in the strength of interactions between the neighboring spins.
So, what is a phase transition? If you’ve ever watched an ice cube melt into liquid water, then you’ve witnessed one first hand. When the ice molecules reach melting temperature, they enter into a kind of intermediate state, where they are essentially unsure of whether they want to remain in the rigid crystalline structure of the ice cube, or enter into the more chaotic state of water’s liquid phase. The transformation that turns ice into liquid water is a phase transition.
Simulating the phase transition of the GHZ state from long-range order to disorder and back again is kind of like taking an ice cube, melting it, and freezing it again. However, instead of being made up of water molecules, the GHZ state is made up of “spins.” In an Ising model system, you can think of a spin as an atom-sized magnet arranged into a grid-like structure or “lattice” with other spins to make up some larger magnetic material. The spin can point in one of two directions, either up or down.
Physicists are often interested in the question of whether the spins in a lattice all want to be aligned, or if they all want to be random. In the 1970s, theoretical physicist Hidetoshi Nishimori identified the now famous Nishimori line, which illustrates this transition from order to disorder in spin glass models
What is a spin glass? A spin glass is a type of magnetic state that is studied in condensed-matter physics. It is characterized by disorder and random interactions between individual spins within the system.
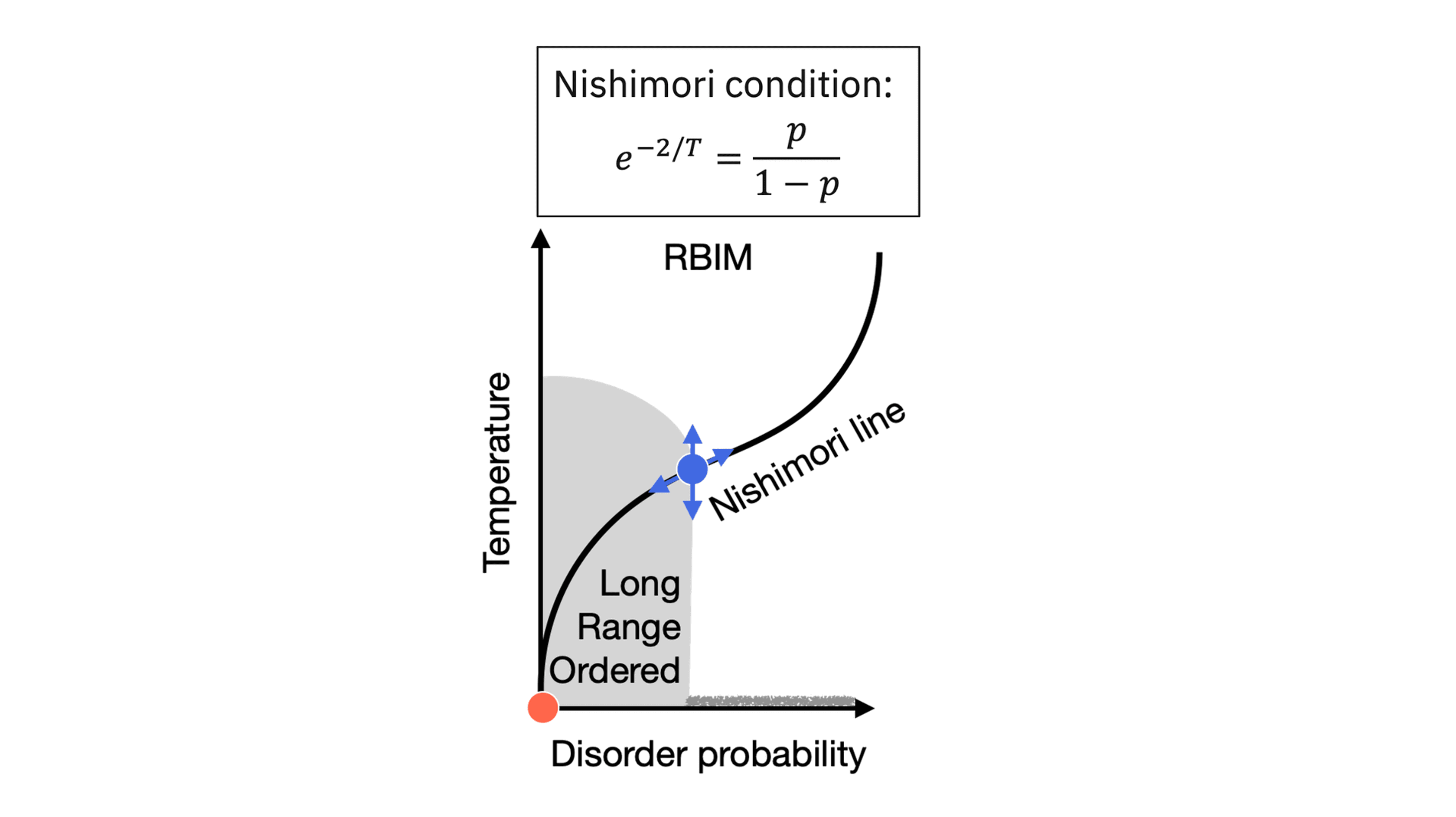
A long-range ordered system is, as you might guess, a system in which the spins are all aligned in either the spin up state or the spin down state. When we increase the system’s temperature or disorder probability, we push it from the long-range ordered phase into the disordered phase—with the system following the path of the Nishimori line. The crossover point between long-range order and disorder, marked in the figure above in blue, is known as the Nishimori transition or the Nishimori “criticality.” The red point marked at the bottom of the chart is the GHZ state.
As far as we know, creating a truly long-range ordered state in a real magnetic material is not possible because it would require actively tuning the individual atomic-scale properties of the material. Real magnets always have tiny imperfections—individual atoms whose spin does not align with the rest of the system. In our Nature Physics experiment, however, we showed that we can use the qubits in an IBM quantum computer to simulate the interaction between spins in a lattice, and dynamically tune the individual magnets within the lattice to realize the phase transition between disorder and long-range order.
Prior to this experiment, it was unknown whether this kind of tuning could be performed in the presence of measurement error. Our research shows that is possible to manipulate the spin degree of freedom in qubits in a controllable way, much like we boil water by applying heat, and we were able to do this in a quantum computer despite the fact that our implementation of this phase transition is inherently noisy.
Realizing the GHZ state and the Nishimori transition in superconducting quantum circuits
We ran our simulation experiments on ibm_sherbrooke, a 127-qubit IBM Quantum Eagle processor. To create the GHZ state with their measurement-based protocol, we begin by dividing the processor’s qubits into two categories—the system qubits that will make up the GHZ state, and the auxiliary qubits that serve to prepare and measure the GHZ state. In the image below, you can see how we divided up the processor’s qubits for our largest simulation, which we ran on 125 of the ibm_sherbrooke’s 127 qubits:
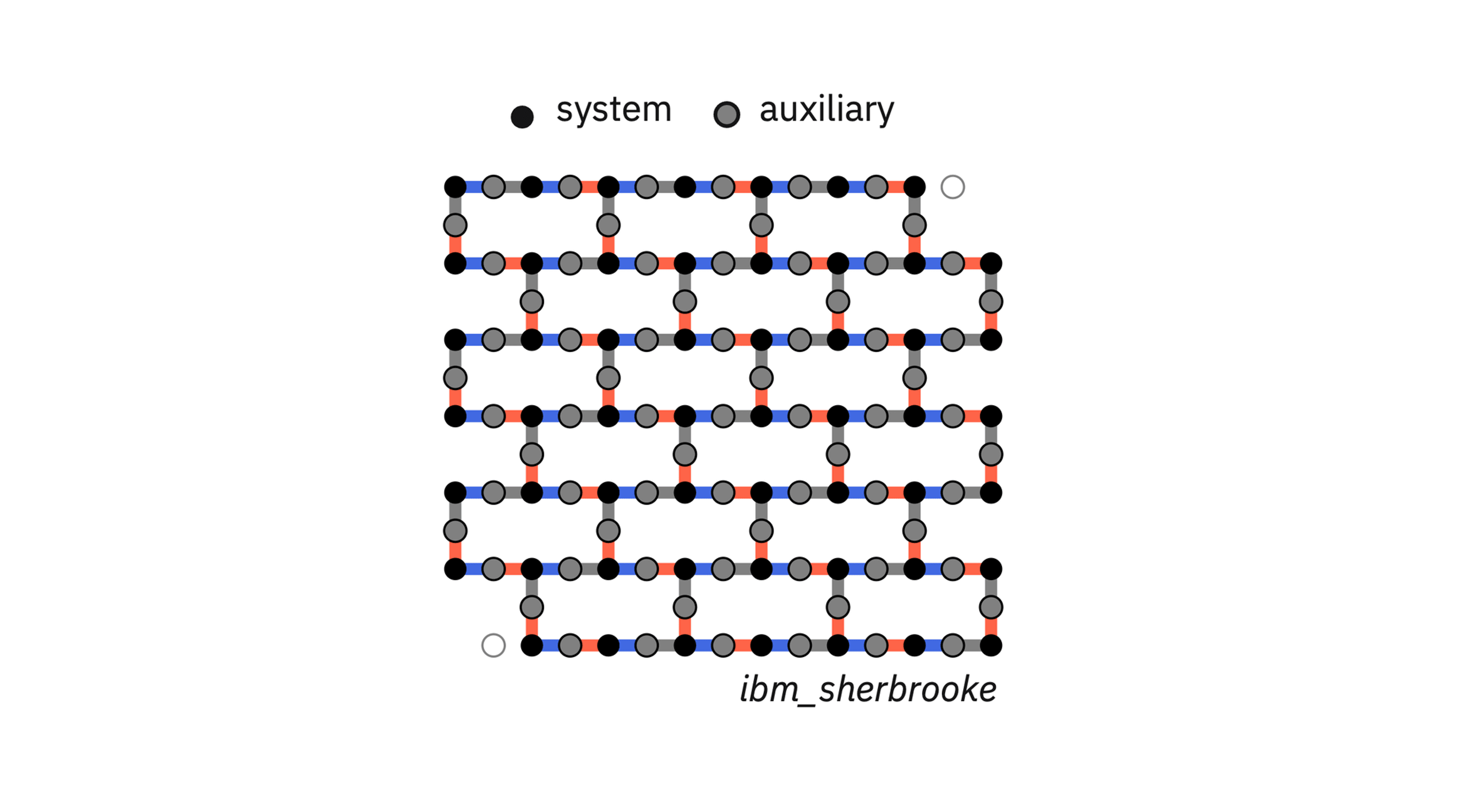
As you can see, the system qubits that will represent the GHZ state are colored black, while the auxiliary qubits are colored gray. Gray auxiliary qubits are placed in between each of the black system qubits so that no two system qubits are directly adjacent. You’ll also notice some color coding in the physical connections or “bonds” that connect each qubit to its nearest neighbors. The bonds are divided into three groups—blue, red, and gray. This detail will be important for executing the circuit protocol.
The protocol begins with all qubits initialized into the ground state. In a perfect, error-free world, we could create a GHZ state without using any auxiliary qubits or mid-circuit measurements at all. We would simply initialize the system qubits, use purely unitary, two-qubit entangling gates to entangle each pair of neighboring qubits, and measure the qubits at the end of this simple circuit to reveal the desired long-range ordered state.
Of course, we do not live in an error-free world. Gate errors, measurement errors, and other kinds of error inevitably throw the system out of long-range order, or prevent us from determining whether long-range order has been achieved. That’s where the auxiliary qubits play a role. To better understand their purpose, let’s zoom in on a small sub section of the processor’s qubits—two system qubits connected by an auxiliary qubit in between them:
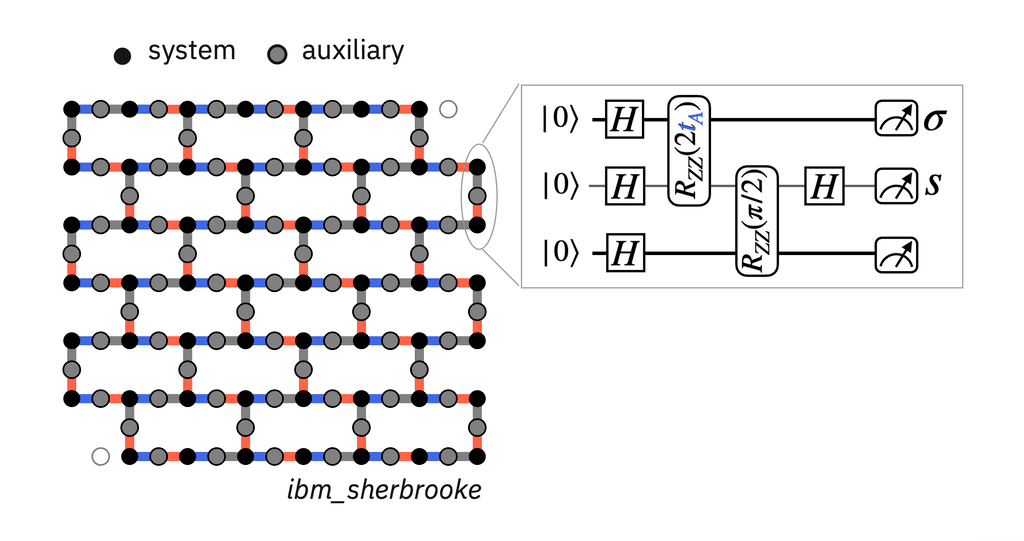
We begin the protocol by applying separate Hadamard gates to each individual qubit, preparing all three qubits in their own separate superposition states. Our goal is to entangle the two system qubits, which we do by applying two qubit gates. However, in superconducting quantum processors, we can only apply two qubit gates to qubits that are directly adjacent to each other, and the system qubits are separated by the auxiliary qubit that sits in between them. To connect the two system qubits, we’ll need to perform a simple quantum teleportation experiment.
First, we entangle each of the system qubits to the auxiliary qubit using local unitary two-qubit gates. At this point, all three qubits are highly entangled - but we only need the two system qubits to be entangled. So we apply another Hadamard gate to the auxiliary qubit, which upon measurement, creates a maximally entangled Bell pair between the two adjacent system qubits.
We can extend this small, three-qubit example to all system qubits, performing the same entangling operations across all system qubits and the auxiliary qubits that sit in between them. More specifically, we first apply our two-qubit gates simultaneously to all qubits connected by gray-colored bonds, then to all qubits connected by red-colored bonds, and finally to all qubits connected by blue-colored bonds. This method allows us to maintain constant-depth in the circuit and avoid introducing unnecessary complexity. It also creates a macroscopic GHZ state across all system qubits with the auxiliary qubits serving as bridges for the entanglement.
This raises two important questions:
- How do we actually verify that we have made the transition from disorder to long-range order?
- How can we observe the nature of this phase transition and determine whether it follows the famous Nishimori line?
To answer the first question, all we have to do is projectively measure all auxiliary qubits, and feed those measurement outcomes into a function on a classical computer that allows us to decode the state of the remaining system qubits. This classical decoder helps us verify that the system qubits have achieved the long-range order of the GHZ state.
To probe the nature of this phase transition from disordered to ordered, we can manually inject errors into the circuit—both the coherent errors that distort interactions between qubits, and the incoherent errors that corrupt the communications channel between the quantum computer and the classical decoder. This gives us the ability to observe how the quantum state evolves as the disorder probability is tuned up and down. The macroscopic behavior of all pair-wise correlations in the system, upon injecting both types of errors, reveals that our quantum state follows the same path as the Nishimori line:
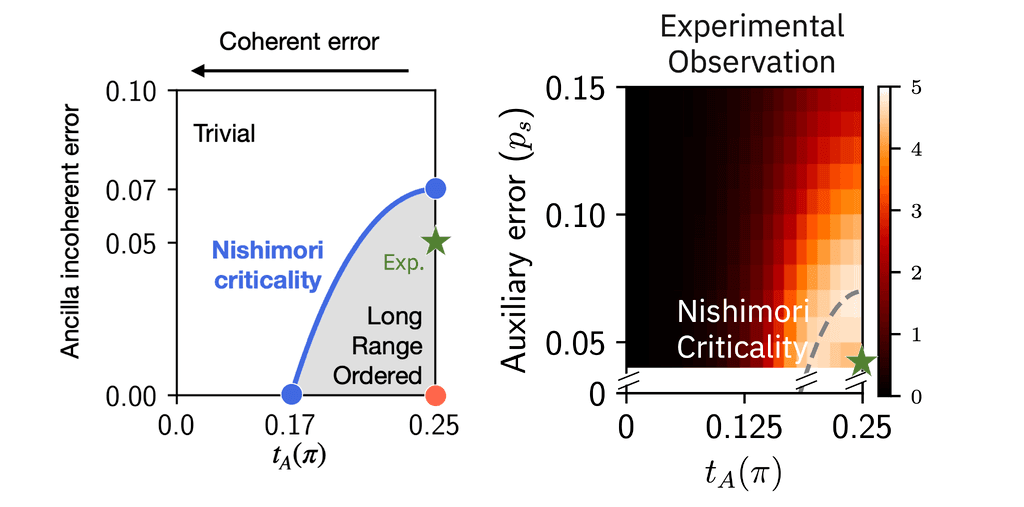
This work shows not only that it is possible to create and manipulate the phase transition between order and long-range order on a quantum computer, but also demonstrates our ability to do so at scale, given that our largest experiment simulates up to 54 spins across 125 qubits. Our theory work indicates that this protocol could even scale up to 1,121 qubits using a larger device like the IBM Quantum Condor.
How a condensed-matter physics experiment reveals insights into the nature of quantum information
At its core, our simulation experiment is a powerful example of the impact quantum computers can make in condensed-matter physics research. This work is the first to show that we can manipulate the error in quantum hardware to transition a quantum system into and out of long-range order in a controlled way.
Given that our simulations concern the random bond Ising model—an important model of magnetism—this could have important implications for our understanding of real-world magnetic materials, revealing insights into how it is possible for them to maintain their magnetic effects despite the presence of imperfections in their atomic structure.
Magnetism is an important field in physics because magnets are pervasive in technology. We use them in smartphones, hard drives, and MRI medical scans—to name just a few examples—and a better understanding of magnetism is essential for progress in the semiconductor processing that we use to create computer chips.
However, this work may also have more fundamental relevance for our understanding of quantum information. In the early 2000s, theorists from Caltech drew a profound connection between the random bond Ising model and quantum error correcting codes. At the time, the question of whether practical quantum error correction could ever be achieved was much more controversial than it is today.
By mapping quantum errors to spins and their interactions in the random bond Ising model, the Caltech researchers rigorously proved that small amounts of quantum errors are not detrimental to quantum information—in the same way that low-enough levels of magnetic disorder do not immediately ruin long-range magnetic ordering. Through this connection, they established that quantum computers can indeed tolerate a certain amount of error.
Another interesting takeaway is the simple but perhaps counterintuitive fact that quantum information is not always exclusively quantum in nature; it can co-exist with classical information. In our experiments, we used a classical decoder to take information from the classically projected auxiliary qubits, and then used that classical information to recover quantum information that was previously hidden. This shows that, at least in some cases, we cannot process quantum information successfully without also processing classical information.
This goes against some of the basic intuitions we develop as students of quantum information science when we learn about fundamental concepts like the observer effect, which tells us that the act of observing or measuring a quantum state collapses the state’s quantum information into classical information. We often see this concept illustrated via the famous Schrödinger’s cat thought experiment, where a cat trapped in a box with a radioactive isotope exists in a superposition state of “alive” and “dead” until an observer looks inside the box. The act of observation forces the state of the cat to settle into one of the two classical options.
Nature, however, is a bit more complicated. This research shows that, in the real world, when you have a quantum state and want to get a glimpse inside it, you can collapse part of that state through measurement, and use the classical information you collect from that measurement to learn something about the quantum information that has yet to be directly measured. These sorts of measurement-based protocols could play an important role towards the development of algorithms for studying condensed-matter phenomena using quantum processors.
For more details on this experiment, be sure to read the full paper in Nature Physics. To learn how to replicate the experiment for yourself, be sure to check out our tutorial on IBM Quantum Learning.




