At what cost can we simulate large quantum circuits on small quantum computers?

Over the course of the past year, the IBM Quantum team has begun researching a host of computational methods called circuit knitting. Circuit knitting techniques allow us to partition large quantum circuits into subcircuits that fit on smaller devices, incorporating classical simulation to “knit” together the results to achieve the target answer. The cost is a simulation overhead that scales exponentially in the number of knitted gates.

Circuit knitting will be important well into the future. Our quantum hardware development team is focused on scaling by connecting smaller processors via classical, and then via quantum links. Due to this planned hardware architecture, circuit knitting will be useful in the near future as we run problems on classically parallelized quantum processors. Techniques that boost the number of available qubits will also be relevant far into the future.

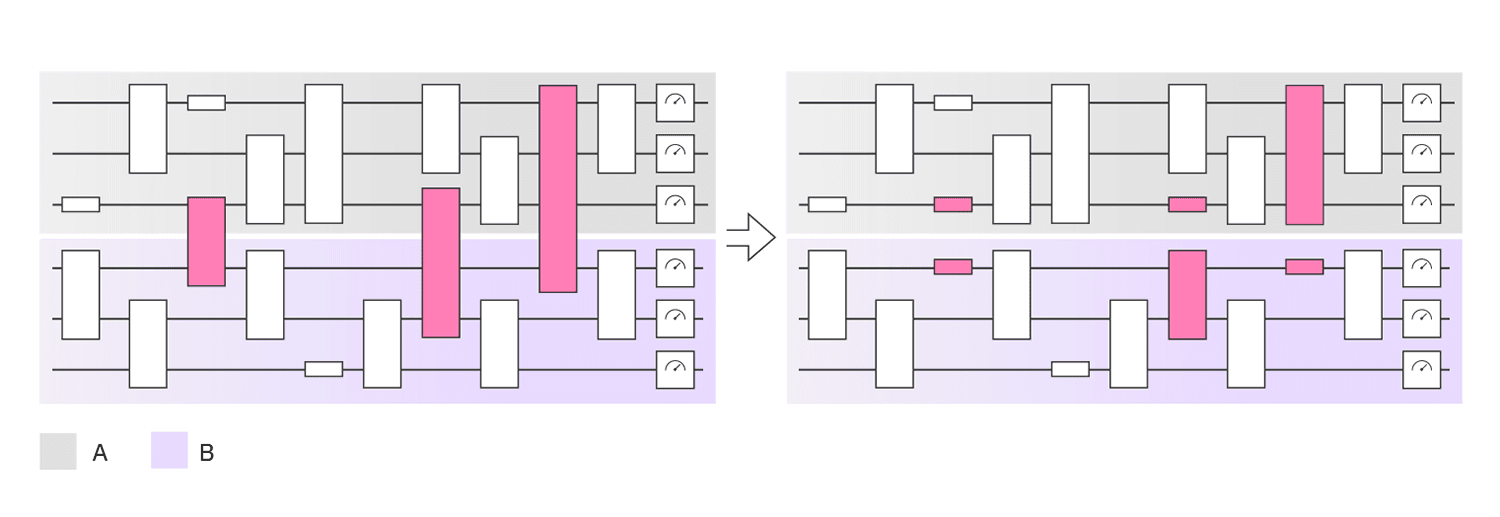
Figure 1: Circuit knitting example: The nonlocal circuit on the left acting on A⊗B can be simulated with local circuits acting only on A or B on the right followed by classical postprocessing.

But first, our team needed to understand how much of a benefit these methods can offer, especially when we knew that the simulation overhead scales exponentially with the number of gates acting between these subcircuits.

We are currently investigating whether classical communication between local quantum computers can help to lower the simulation overhead — as you might see on a pair of classically parallelized IBM Quantum “Heron” processors. Specifically, we realized circuit knitting via a method that has previously gained interest in the fields of error mitigation and classical simulation algorithms, called the quasiprobability simulation technique.¹

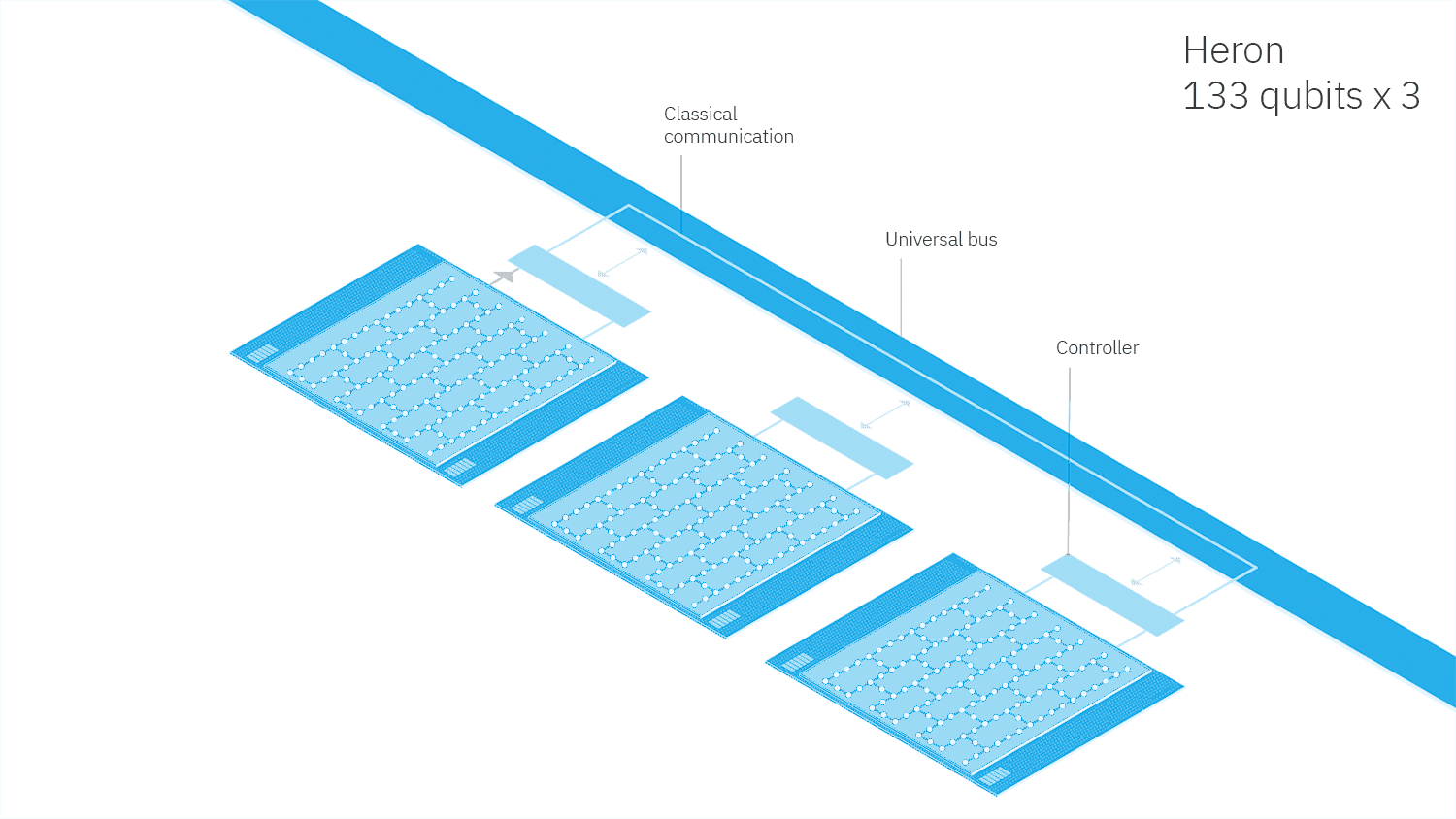
The 133-qubit “Heron” processor, slated for 2023.

We consider three settings to simulate a non-local circuit with local operations. In the first, the two quantum computers can only run their own local operations on their subcircuits without communication between them. In the second the two computers can realize those local operations, with the added ability to send classical information in one direction — from $\Alpha$ to $\Beta$, but not from $\Beta$ to $\Alpha$. In the third, the two quantum computers can run their own local quantum operations and send classical information in either direction between them.

In the local and one-way classical communication settings, one does not necessarily require two separate quantum computers. Instead, one can run the two subcircuits in sequence on the same device. The classical communication in the one-way setting can then be simulated by classically storing the bits sent from $\Alpha$ and $\Beta$. 

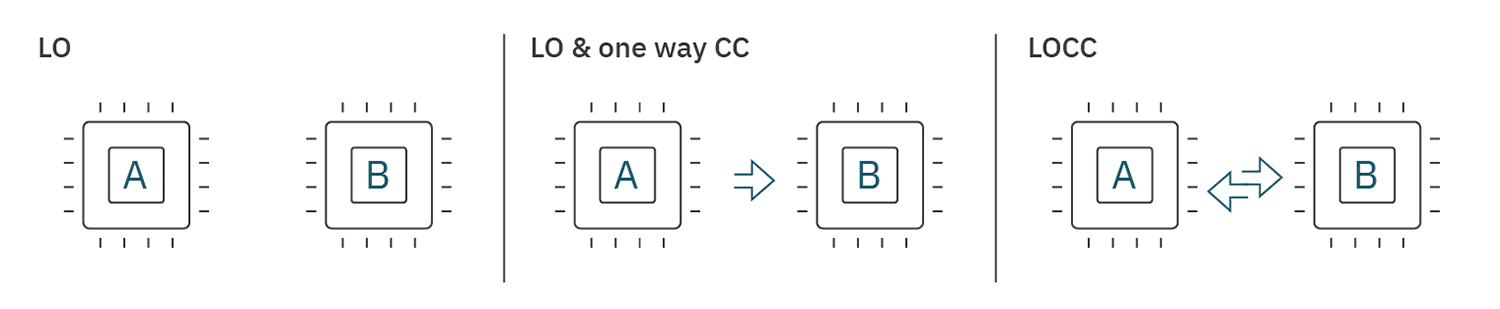
Figure 2: Graphical overview of the three scenarios considered to run a nonlocal operation. LO refers to local operations; LO & one way CC refers to local operations and one way classical communication; LOCC refers local operations and classical communication.

In contrast, the two-way communication setting requires two quantum computers that exchange classical information in both directions. We show that for circuit knitting based on quasiprobability simulation, the three settings mentioned above all have a different sampling overhead when applied to circuits with multiple instances of the same non-local gate. 

Our results, available on arXiv,² demonstrate that two-way communication can considerably reduce the simulation overhead. For circuits containing n CNOT gates connecting each subcircuit, the incorporation of classical information exchange between the subcircuits reduces the simulation overhead from O(9ⁿ) to O(4ⁿ) — a reduction that is substantial in practice. It allows us to cut considerably more CNOT gates — that is, the gates that entangle the qubits — for a given fixed simulation overhead.

On a technical level, our results are based on the insight that a simultaneous local preparation of two maximally entangled states, called Bell pairs, is more efficient than locally preparing a single Bell pair twice. The reason is that for a joint preparation we can make use of entanglement between the local subsystems, which is not possible if we prepare the two Bell pairs separately. Using the idea of gate teleportation we can then convert Bell pairs into CNOT gates under local operations and classical communication.

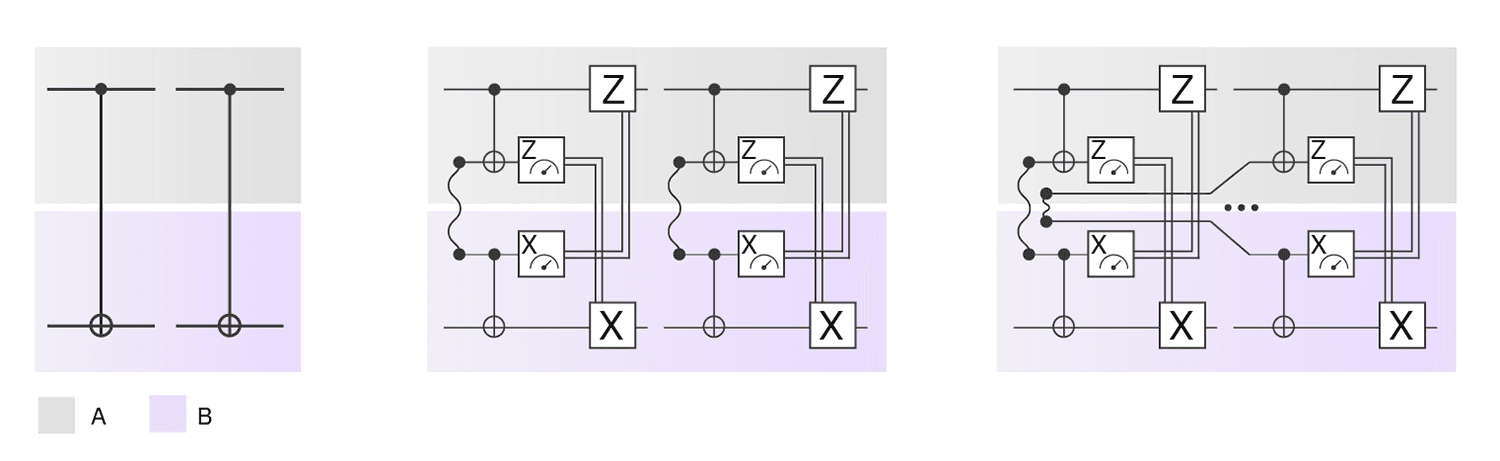
Figure 3: Graphical explanation of how to realize two CNOT gates in a LOCC setting via gate teleportation. By generating the two Bell pairs simultaneously (instead generating twice a single Bell pair), we can reduce the total simulation overhead.

Our results show that classical communication between locally separated quantum computers is beneficial when performing large computations that exceed the number of qubits each quantum device individually has.

Following the latest IBM roadmap, these results may be helpful in reducing simulation overheads in future architectures as it motivates the connection of individual quantum chips with classical communication links.

Learn more about:

Quantum Circuits and Software: Our software team works alongside the hardware developers to build an expansive library of quantum circuits and to create programming tools so that anyone can develop their own quantum software.