In this video, originally filmed in 2018, IBM Fellow Charles H. Bennett gives a vivid breakdown of the formulation and implications of quantum computing.
Bennett, an IBM Fellow, joined the company in 1972 to study the energy cost of computation. He quickly made an impression in the field when his 1973 paper, Logical reversibility of computation,1 showed that by making computers logically reversible, so that no two distinct logical states have the same successor, they may be made thermodynamically reversible, and thus capable of accomplishing an unlimited amount of number crunching per unit of physical energy dissipated.
Turing machines may be made logically reversible at every step, while retaining their simplicity and their ability to do general computations.
Bennett was also behind the 1984 breakthrough in quantum cryptography,2 and the 1993 discovery of quantum teleportation.3
In 1984, Charles H. Bennett and the Université de Montréal’s Gilles Brassard developed a quantum cryptographic scheme they called BB84, which allowed secure communication between parties that do not initially share secret information.
And in one moment of seminal quantum history, the 1981 Physics of Computation Conference at MIT, he was literally behind the camera, taking the picture:
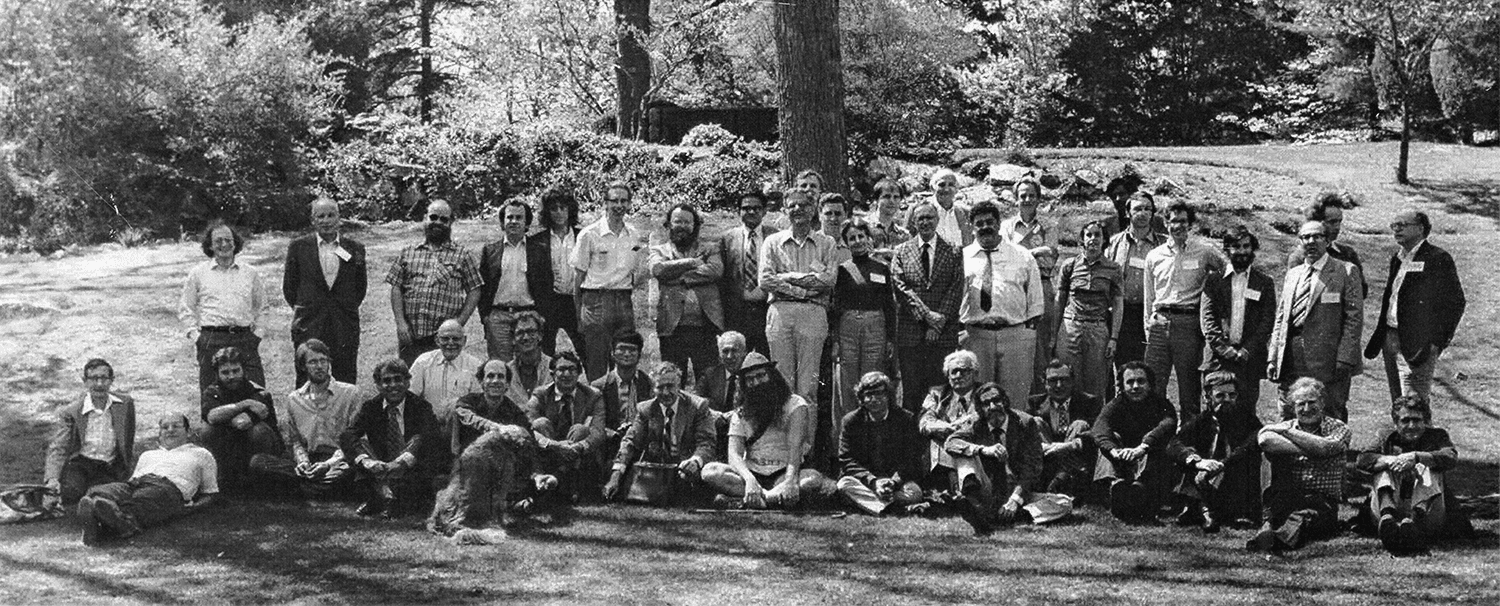
1981 IBM-MIT Physics of Computation Conference. (Photo courtesy of Charles H. Bennett.)
In the following Q&A, we ask Bennett about his career, the moments that have helped turn quantum information science from theory to present-day computing reality, and the progress he hopes to see in the coming years.
What made you decide to incorporate quantum into your work at IBM?
Fifty years ago, as today, people wished computers would consume less energy and generate less waste heat. [IBM Fellow] Rolf Landauer recruited me to IBM Research because I shared his interest in whether there was a fundamental thermodynamic limit to the energy efficiency of computers. Together, we answered this question in the negative.
That success, and IBM’s encouragement of curiosity-driven research, got me thinking about other aspects of informational physics. The IBM Thomas J Watson Research Center lab, then 60% its current size , was a hotbed of interaction between pure and applied science, and between physics and math, where I learned about computational complexity and algorithmic information theory from the likes of IBM scientists Mark Wegman and Gregory Chaitin, and critical phenomena from Erling Pytte and Geoff Grinstein. I began thinking and telling them about Stephen Wiesner’s discoveries of classically impossible information processing tasks that could be accomplished using quantum physics.
What quantum breakthrough over the last 50 years are you most intrigued by?
It’s not one big breakthrough, but multiple interlocking advances, like Wiesner’s discovery of information processing tasks (impossible-to-counterfeit banknotes, and a way to multiplex two messages into a transmission from which the receiver could receive either one, but not both) that are classically impossible but enabled by quantum physics. These led Université de Montréal’s Gilles Brassard and me to develop quantum cryptography, the first practical application of quantum information.
The no-cloning theorem, and the fact that entanglement, while having no ability to communicate by itself, is a quantifiable resource that can assist both classical and quantum communication, e.g. in quantum teleportation. Peter Shor’s discovery of a dramatic quantum speedup for practically important problems.
The Story Behind Shor's Algorithm
The discovery and development of quantum error-correcting codes, which along with the Solovay-Kitaev theorem, made scalable fault-tolerant quantum computers possible in principle.
Based on these advances, the rebuilding of the entire theory of communication, computation, interaction, and privacy on a quantum foundation was possible — so a classical channel is a quantum channel with an eavesdropper, and a classical computer is a quantum computer subtly handicapped by having eavesdroppers on all its wires; [as well as] the essential role of entanglement and no-cloning in the emerging understanding of black holes and quantum gravity; and the 2020 result MIP*=RE unexpectedly connecting entanglement with computability theory.
One can only guess how this radically deepened understanding of information will change everyday life. My guess is more subtly than classical IT already has, but enough to justify the pace and scale of research in quantum science and engineering, at IBM and elsewhere, have aimed at finding out.
What does your recognition and election to the Royal Society mean for the field of quantum theory, and computation?
It may help the average person to see quantum laws and phenomena as an important aspect of the universe whose essence they can understand, rather than as incomprehensible weirdness about to revolutionize everything.
What inspires you to take photographs at the conferences you’ve attended?
I’ve always thought of old photos and ephemera as an important window on the past, through which we can see things people were unaware of at the time. They pique our curiosity about aspects of our current worldview that are hidden from us because we are in the middle of it, though they may become evident later to future viewers of the photograph.

IBM Fellow Charles H. Bennett signing the Royal Society members’ book.
Charles H. Bennett’s accolades
- 2020 Claude E Shannon Award
- 2019 BBVA Frontiers of Knowledge Award in Basic Sciences
- 2019 Micius Quantum Prize
- 2018 Wolf Prize Laureate in Physics
- 2017 International Center for Theoretical Physics Dirac Medal
- 2011 Winner, Okawa Prize
- 2008 Winner, Harvey Prize
- 1998 Fellow of the American Physical Society
- 1997 Member of the National Academy of Sciences




